直線と直線の交点に関する例題について見ていきます。
①平行(交わらない) ②ねじれの位置(交わらない) ③交点をもつ
の3つのパターンとなります。①の特殊例として2直線が一致するということもあります。
(例題1)
\(A(-5,3,3)\), \(B(-4,1,5)\) を通る直線\(l\)と、\(C(0,3,2)\), \(D(3,7,-3)\) を通る直線\(m\)の交点の座標を求めよ。
(解答)
\(s,t\)を実数とする。
\(A(-5,3,3)\), \(B(-4,1,5)\) を通る直線\(l\)の方程式は
\(\vec{p}=(-5,3,3)+s(1,-2,2)=(-5+s,3-2s,3+2s)\)・・・①
\(C(0,3,2)\), \(D(3,7,-3)\) を通る直線\(m\)の方程式は
\(\vec{p}=(0,3,2)+t(3,4,-5)=(3t,3+4t,2-5t)\)・・・②
①②の成分が一致するような実数\(s,t\)が存在すれば、そのとき交点の座標となる。
\(-5+s=3t\)・・・③
\(3-2s=3+4t\)・・・④
\(3+2s=2-5t\)・・・⑤
④⑤より \(s=2\), \(t=-1\)
これは③を満たす
よって交点の座標は①に\(s=2\)を代入して
\((-3,-1,7)\)
(例題2)
2点 \(O(0,0,0)\) \(A(0,2,1)\) を通る直線を\(l_1\)、2点 \(B(1,0,2)\), \(C(2,1,0)\) を通る直線を\(l_2\)とするとき、直線\(l_1\)と直線\(l_2\)は交わらないことを示せ。
(解答)
\(s,t\)を実数とする。
\(O(0,0,0)\) \(A(0,2,1)\) を通る直線\(l_1\)の方程式は
\(\vec{p}=(0,0,0)+s(0,2,1)=(0,2s,s)\)・・・①
\(B(1,0,2)\), \(C(2,1,0)\) を通る直線\(l_2\)の方程式は
\(\vec{p}=(1,0,2)+t(1,1,-2)=(1+t,t,2-2t)\)・・・②
①と②の成分を比較して
\(0=1+t\)・・・③
\(2s=t\)・・・④
\(s=2-2t\)・・・⑤
③より \(t=-1\)
これと④より \(s=-\displaystyle\frac{1}{2}\)
しかし、\(s=-\displaystyle\frac{1}{2}\), \(t=-1\) は⑤を満たさない。
よって成分が一致するような実数\(s,t\)が存在しないので、交点をもたない。
(例題3)
点\(O\)を原点とする座標空間の3点を \(A(0,1,2)\), \(B(2,3,0)\), \(P(5+t,9+2t,5+3t)\) とする。線分\(OP\)と線分\(AB\)が交点をもつような実数\(t\)が存在することを示せ。また、そのとき、交点の座標を求めよ。
例えば線分\(AB\)については、表し方は媒介変数を1つ or 2つ 使うかで
(1)\(\overrightarrow{OQ}=\overrightarrow{OA}+t\overrightarrow{AB}\) のとき、\(A\)から\(B\)までの移動を考えて \(0≦t≦1\)
(2)\(\overrightarrow{OQ}=s\overrightarrow{OA}+t\overrightarrow{OB}\), \(s+t=1\) のときは \(s≧0\), \(t≧0\)
解答では(1)の方針で解いてきますが、問題文で\(t\)が使われているので別の文字でやっていきます。詳しくは平面の分野ですが内容は同じなので →(5-5)軌跡領域① を参照してください。
(解答)
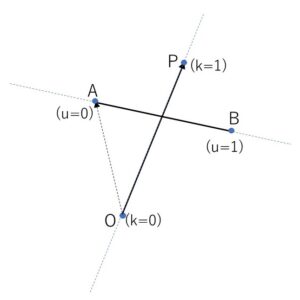
線分\(AB\)上の点を\(Q\)とすると
\(\overrightarrow{OQ}=\overrightarrow{OA}+u\overrightarrow{AB}\) (\(0≦u≦1\))
よって、\(A(0,1,2)\), \(B(2,3,0)\) より
\(\overrightarrow{OQ}=(0,1,2)+u(2,2,-2)\)\(=(2u,1+2u,2-2u)\)・・・①
線分\(OP\)上の点を\(R\)とすると
\(\overrightarrow{OR}=k\overrightarrow{OP}\) (\(0≦k≦1\))
よって、\(P(5+t,9+2t,5+3t)\) より
\(\overrightarrow{OR}=(5k+kt,9k+2kt,5k+3kt)\)・・・②
\(\overrightarrow{OQ}=\overrightarrow{OR}\) となる \(u,k\) 及び \(t\) が存在すれば線分が交点をもつ。①②の成分を比較して
\(2u=5k+kt\)・・・③
\(1+2u=9k+2kt\)・・・④
\(2-2u=5k+3kt\)・・・⑤
③④より\(kt\)を消去して
\(2u-1=k\)・・・⑥
③⑤より\(kt\)を消去して
\(8u-2=10k\)・・・⑦
⑥⑦より
\(u=\displaystyle\frac{2}{3}\), \(k=\displaystyle\frac{1}{3}\)
(\(0≦u≦1\), \(0≦k≦1\) を満たす)
よって③より
\(\displaystyle\frac{4}{3}=\displaystyle\frac{5}{3}+\displaystyle\frac{1}{3}t\)
\(t=-1\)
したがって交点をもつような \(t(=-1)\) が存在して、①に\(u=\displaystyle\frac{2}{3}\)を代入するとその座標は
\((2u,1+2u,2-2u)=\)\((\displaystyle\frac{4}{3},\displaystyle\frac{7}{3},\displaystyle\frac{2}{3})\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→点と直線の距離、直線と直線の距離 back→直線の方程式