点と直線の距離、直線と直線の距離

点と直線の距離、直線と直線の距離に関する例題について見ていきます。

(例題1)
直線\(g:(x,y,z)=(3,1,2)+t(2,2,1)\) と 点\(A(2,-3,3)\) について、次の問いに答えよ。
(1)点\(A\)と直線\(g\)の最短距離を\(d\)とするとき、\(d\)を与える\(g\)上の点\(H\)の座標および\(d\)を求めよ。
(2)直線\(g\)に関して点\(A\)と対称な点\(B\)の座標を求めよ。

(解答)
(1)

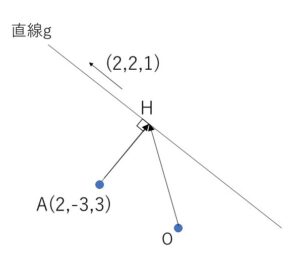
\(H\)は\(A\)から直線\(g\)に下ろした垂線の足である。

\(\overrightarrow{OH}=(3,1,2)+t(2,2,1)=(3+2t,1+2t,2+t)\)・・・①
\(\overrightarrow{AH}=\overrightarrow{OH}-\overrightarrow{OA}\)
\(=(1+2t,4+2t,-1+t)\)・・・②

直線の方向ベクトルを \(\vec{v}=(2,2,1)\) とすると

\(\overrightarrow{AH}\cdot\vec{v}=0\) より
\(2(1+2t)+2(4+2t)+(-1+t)=0\)
\(t=-1\)

よって①より\(H\)の座標は
\((3+2t,1+2t,2+t)=\)\((1,-1,1)\)

また②より
\(\overrightarrow{AH}=(-1,2,-2)\) だから

\(d=|\overrightarrow{AH}|\)
\(=\sqrt{(-1)^2+2^2+(-2)^2}\)
\(=3\)

(別解)
(2点間の距離を求めて、最小値を考えると)
\(\overrightarrow{OH}=(3,1,2)+t(2,2,1)=(3+2t,1+2t,2+t)\)

\(A(2,-3,3)\), \(H(3+2t,1+2t,2+t)\)・・・① より

\(AH^2=(2t+1)^2+(2t+4)^2+(t-1)^2\)
\(=9t^2+18t+18\)
\(=9(t+1)^2+9\)

よって \(t=-1\) のとき \(d=AH=3\) であり
①より \(H(1,-1,1)\)

(2)

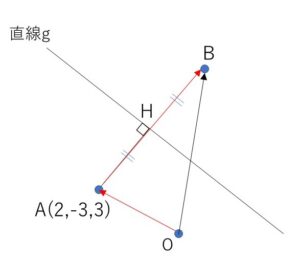
\(B\)は\(AH\)の延長線上にあり、\(AH=BH\)
(1)より　\(\overrightarrow{AH}=(-1,2,-2)\) だから

\(\overrightarrow{OB}=\overrightarrow{OA}+2\overrightarrow{AH}\)
\(=(2,-3,3)+2(-1,2,-2)\)
\(=(0,1,-1)\)

したがって
\(B(0,1,-1)\)

(例題2)
空間内に2つの直線
\(l_1:(x,y,z)=(1,1,0)+s(1,1,-1)\)
\(l_2:(x,y,z)=(-1,1,-2)+t(0,-2,1)\)
がある。ただし\(s,t\)は媒介変数である。\(l_1,l_2\)上にそれぞれ点\(P,Q\)をとるとき、線分\(PQ\)の長さの最小値を求めよ。

(解答)
\(\overrightarrow{OP}=(1+s,1+s,-s)\)
\(\overrightarrow{OQ}=(-1,1-2t,-2+t)\) より

\(PQ^2=(-s-2)^2+(-s-2t)^2+(s+t-2)^2\)
\(=3s^2+6st+5t^2-4t+8\)

(自由に動く(独立な)2変数の2次式の最小値なので、平方完成)

\(=3(s+t)^2-3t^2+5t^2-4t+8\)
\(=3(s+t)^2+2(t-1)^2+6\)
\(≧6\)

よって\(PQ\)の最小値は \(s+t=0\), \(t=1\) のとき (\(s=-1,t=1\)のとき)
\(\sqrt{6}\)

(参考)
\(PQ\)が、「2直線\(l_1,l_2\)に垂直になるとき」に最小となることを利用しても解けます。

\(l_1,l_2\)はねじれの位置にあるとします。(交われば距離の最小値は\(0\)で、平行ならば垂直になるときに最小となるのは明らか)

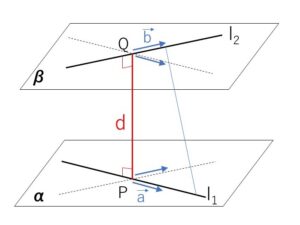
まず直線\(l_1\)を含む平面を\(α\)、直線\(l_2\)を含む平面\(β\)とすると、\(α\)や\(β\)のとりかたは無数に存在しますが、そのうち\(α,β\)が平行になるものを選びます。直線\(l_1,l_2\)の方向ベクトルをそれぞれ\(\vec{a},\vec{b}\)とすると、どちらの平面も\(\vec{a},\vec{b}\)で作られる平面で、それぞれ\(l_1,l_2\)を含んでいるので平行になるような平面の選びかたは1つに定まります。2つの平行な平面は、ちょうど水平な床と天井のような関係にあります。

ここで、この2つの平面の距離は、一方の平面上の点からもう一方の平面に下した垂線の長さ\(d\)になりますが、例えば\(l_2\)を垂線方向に沿って平行移動させると(影を落とすようにしてもよい)、\(l_1\)と\(l_2\)は平面\(α\)で交わることになるので、2点\(P,Q\)の距離で2平面の距離\(d\)と同じになるようなものが存在することになります。\(l_1,l_2\)はそれぞれ平面\(α,β\)に含まれているので、\(PQ\)が2直線\(l_1,l_2\)に垂直にならない場合には\(d\)より大きくなってしまいます。

したがって、最小値をとるときは\(PQ\)が\(l_1,l_2\)に垂直になるときです。

これらのことを利用して解くと、
\(l_1:(x,y,z)=(1,1,0)+s(1,1,-1)\)
\(l_2:(x,y,z)=(-1,1,-2)+t(0,-2,1)\)
\(l_1,l_2\)上の点がそれぞれ\(P,Q\)より

\(\overrightarrow{OP}=(1+s,1+s,-s)\)
\(\overrightarrow{OQ}=(-1,1-2t,-2+t)\)

よって
\(\overrightarrow{PQ}=(-s-2,-s-2t,s+t-2)\)

\(l_1\)の方向ベクトルを \(\vec{a}=(1,1,-1)\)、\(l_2\)の方向ベクトルを \(\vec{b}=(0,-2,1)\) とおくと

\(\overrightarrow{PQ}\cdot\vec{a}=0\),　\(\overrightarrow{PQ}\cdot\vec{b}=0\) より

\((-s-2)+(-s-2t)-(s+t-2)=0\)
\(-2(-s-2t)+(s+t-2)=0\)

整理して
\(-3s-3t=0\)
\(3s+5t-2=0\)

よって
\(s=-1\), \(t=1\)

したがって
\(\overrightarrow{PQ}=(-s-2,-s-2t,s+t-2)\)
\(=(-1,-1,-2)\) だから

\(|\overrightarrow{PQ}|\)
\(=\sqrt{(-1)^2+(-1)^2+(-2)^2}\)
\(=\sqrt{6}\)

ゆえに\(PQ\)の最小値は
\(\sqrt{6}\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→平面の方程式　back→直線と直線の交点