回転体の方程式の求め方について見ていきます。
・回転体の方程式
\(x≧0\) で定義された関数 \(z=f(x)\) を、\(z\)軸回りに1回転させてできた図形の方程式は次のようになります。
\(z=f(\sqrt{x^2+y^2})\)
(解説)
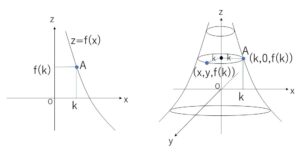
\(zx\)平面における \(A(k,f(k))\) について
\(z=f(k)\)・・・①
\(xyz\)空間において、\(z=f(k)\)における回転体の断面は、半径\(k\)の円になるから
この円周上の点を \((x,y,f(k))\) とすると
\(\sqrt{x^2+y^2}=k\)・・・②
①②より
\(z=f(\sqrt{x^2+y^2})\)
他の軸の回転に関しては同様に適宜考えてください。
・円錐面の方程式
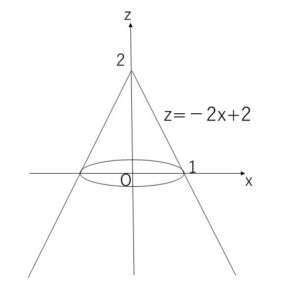
直線 \(z=-2x+2\) (\(x≧0\))
を\(z\)軸回りに回転させてできる図形は円錐になりますが、この円錐面の方程式は上記回転体の方程式より
\(z=-2\sqrt{x^2+y^2}+2\)・・・①
となります。ここで①を変形していくと
\(2\sqrt{x^2+y^2}=2-z\)
左辺は\(0\)以上なので \(z≦2\) となり2乗すると
\(4(x^2+y^2)=(2-z)^2\), \(z≦2\) ・・・②
となります。
ここで、ベクトルの内積を利用した別の方法でも円錐面の方程式を求めてみます。
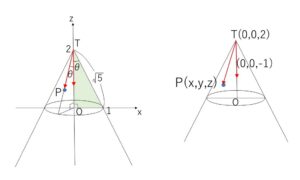
頂点を\(T(0,0,2)\), 円錐面上の点を\(P(x,y,z)\)とおくと、\(\overrightarrow{TP}\)は、円錐の中心軸である\(z\)軸方向とのなす角が\(θ\)で一定です。\(z\)軸方向のベクトルを \(\vec{v}=(0,0,-1)\) とおくと
\(\overrightarrow{TP}\cdot\vec{v}=|\overrightarrow{TP}||\vec{v}|\cosθ\)
\(\overrightarrow{TP}=(x,y,z-2)\), \(\cosθ=\displaystyle\frac{2}{\sqrt{5}}\) より
\(-(z-2)=\sqrt{x^2+y^2+(z-2)^2}\cdot\displaystyle\frac{2}{\sqrt{5}}\)
\(\sqrt{5}(2-z)=2\sqrt{x^2+y^2+(z-2)^2}\)
右辺は\(0\)以上なので、\(z≦2\) であり、2乗すると
\(5(2-z)^2=4\{x^2+y^2+(z-2)^2\}\), \(z≦2\)
よって
\((2-z)^2=4(x^2+y^2)\), \(z≦2\)
と②と同じ式になります。
(例題)
座標空間の原点\(O\)を通りベクトル \((1,\sqrt{3},2\sqrt{3})\) に平行な直線を\(l\)とし、点\(A\)の座標を \((\sqrt{3}+3,3\sqrt{3}+3,6-2\sqrt{3})\) とする。このとき、\(O\)を頂点とする円錐\(C\)は、底面の中心\(H\)が\(l\)上にあり、底面の円周が\(A\)を通るとする。
(1)\(\angle AOH=□π\) である。ただし、\(0≦\angle AOH<π\) とする。
(2)\(H\)の座標は \((□,□,□)\) である。
(3)点\((\sqrt{3},y,z)\) が\(C\)の底面上(境界線を含む)にあるとき、常に \(y+□z+□=0\) が成り立つ。
(4)点\((\sqrt{3},y,z)\) が\(C\)の底面上(境界を含む)にあるとき、常に
\(□y^2+□yz+□z^2+□y+□z+21=0\) が成り立つ。
(解答)
(1)
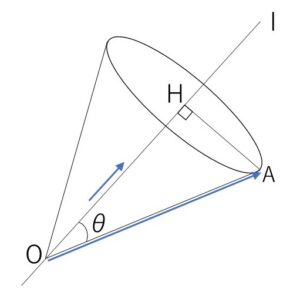
\(\angle AOH=θ\) とおく。
直線\(l\)の方向ベクトルは \(\vec{v}=(1,\sqrt{3},2\sqrt{3})\)
\(\overrightarrow{OA}=(\sqrt{3}+3,3\sqrt{3}+3,6-2\sqrt{3})\) より
\(\cosθ=\displaystyle\frac{\overrightarrow{OA}\cdot\vec{v}}{|\overrightarrow{OA}||\vec{v}|}\)
\(\overrightarrow{OA}\cdot\vec{v}\)
\(=1\cdot(\sqrt{3}+3)+\sqrt{3}(3\sqrt{3}+3)+2\sqrt{3}(6-2\sqrt{3})\)
\(=16\sqrt{3}\)
\(|\overrightarrow{OA}|\)
\(=\sqrt{(\sqrt{3}+3)^2+(3\sqrt{3}+3)^2+(6-2\sqrt{3})^2}\)
\(=4\sqrt{6}\)
\(|\vec{v}|\)
\(=\sqrt{1^2+(\sqrt{3})^2+(2\sqrt{3})^2}\)
\(=4\)
よって
\(\cosθ=\displaystyle\frac{16\sqrt{3}}{4\sqrt{6}\cdot4}\)\(=\displaystyle\frac{1}{\sqrt{2}}\)
したがって
\(θ=\displaystyle\frac{π}{4}\)
(2)
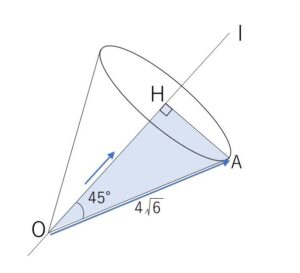
\(OH=OA\cosθ=4\sqrt{6}\cdot\displaystyle\frac{1}{\sqrt{2}}\)
\(=4\sqrt{3}\)
\(\vec{v}=(1,\sqrt{3},2\sqrt{3})\) と同じ方向の単位ベクトルは
\(\vec{v}=\displaystyle\frac{1}{4}(1,\sqrt{3},2\sqrt{3})\) だから
\(\overrightarrow{OH}=4\sqrt{3}×\displaystyle\frac{1}{4}(1,\sqrt{3},2\sqrt{3})\)
\(=(\sqrt{3},3,6)\)
よって \(H(\sqrt{3},3,6)\)
(3)
\(H(\sqrt{3},3,6)\)を通り、法線ベクトルが \(\vec{v}=(1,\sqrt{3},2\sqrt{3})\) である平面の方程式は
\((x-\sqrt{3})+\sqrt{3}(y-3)+2\sqrt{3}(z-6)=0\)・・・①
\(x=\sqrt{3}\) を代入して整理すると
\(y+2z-15=0\)・・・②
平面①上に円錐\(C\)の底面があるので、②が求める式である。
(4)
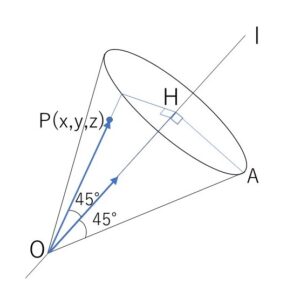
側面上の点を \(P(x,y,z)\) とする。\(\overrightarrow{OP}\) と \(\vec{v}=(1,\sqrt{3},2\sqrt{3})\)のなす角が\(\displaystyle\frac{π}{4}\) だから
\(\overrightarrow{OP}\cdot\vec{v}=|\overrightarrow{OP}||\vec{v}|\cos\displaystyle\frac{π}{4}\)
\(x+\sqrt{3}y+2\sqrt{3}z=\sqrt{x^2+y^2+z^2}\cdot4\cdot\displaystyle\frac{1}{\sqrt{2}}\)
\(x=\sqrt{3}\)を代入して
\(\sqrt{3}(1+y+2z)=\sqrt{3+y^2+z^2}\cdot2\sqrt{2}\)
\(3(1+y+2z)^2=8(3+y^2+z^2)\)
整理して
\(5y^2-12yz-4z^2-6y-12z+21=0\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
back→正射影と空間図形の方程式