正射影と空間図形の方程式

空間図形の2つの方程式から、1文字を消去した方程式の表す図形について見ていきます。

・空間図形の方程式と正射影
次の球面と平面を題材に進めていきます。

\(x^2+y^2+(z-2)^2=1\)・・・① (球面\(S\))
\(x-y-z+2=0\)・・・② (平面\(α\))

球面\(S\)の 半径は\(1\), 中心は \(O_1(0,0,2)\) で、\(O_1\)と平面\(α\)の距離\(d\)は

\(d=\displaystyle\frac{|0-0-2+2|}{\sqrt{1^2+(-1)^2+(-1)^2}}=0<(球の半径1)\)

より平面\(α\)と球面\(S\)は無数の点で交わり、その交線は円になります。

ここで②より
\(z=x-y+2\)
を①に代入して\(z\)を消去すると

\(x^2+y^2+(x-y+2-2)^2=1\)
整理すると
\(2x^2+2y^2-2xy=1\)・・・③
となりますが、③は\(xy\)の項があるので円を表していません。

①②から得られた③式は、平面\(α\)と球面\(S\)の交線(円)に関する何らかの情報があるはずですが、③式は一体何を表しているのでしょうか。

ここで、まず③は\(xy\)平面において楕円の方程式を表していることに着目します。

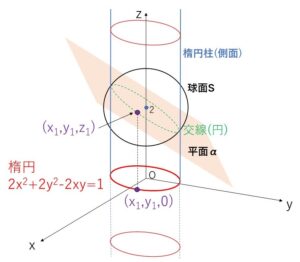
ところで、③は\(xy\)平面上では楕円を表していますが、空間においては楕円柱の側面を表しています。

また、球面\(S\)と平面\(α\)の交線(円)上の点を\((x_1,y_1,z_1)\) とおくと、①②から得られた③式にこの座標を代入しても成り立つので、楕円柱の側面③は\(S,α\)の交線(円)すべてと交わることになります。(楕円柱の側面③を平面②で切断したときの断面が、ちょうど球面①と平面②の交線(円)となっている)

よって交線(円)上の点\((x_1,y_1,z_1)\)について、\((x_1,y_1,0)\) とした点が\(xy\)平面における楕円③上の点になるので、交線(円)に上から光を当ててできた影がこの楕円③になるという関係になっています。

つまり、①②から\(z\)を消去してできた③式は\(xy\)平面においては、①②の交線に上から光を当てて\(xy\)平面へ映した影(正射影)を表す方程式ということになります。

同様に、\(y\)を消去すると\(zx\)平面への正射影、\(x\)を消去すると\(yz\)平面への正射影を表す方程式になります。

以上の議論を座標平面においても検討してみます。

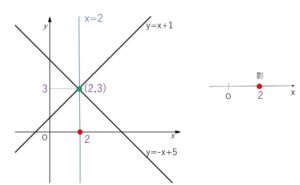
直線 \(y=x+1\)・・・(1)
直線 \(y=-x+5\)・・・(2)

について、(1)を(2)に代入して\(y\)を消去すると
\(x+1=-x+5\)
つまり
\(x=2\)・・・(3)

となりますが、(3)は座標平面上では\(x\)軸に垂直な直線になり、これが先ほどの楕円柱に相当します。(3)を \(y=0\) つまり、ただの数直線上(\(x\)軸)で考えると、\(x=2\) という点を表すことになり、これが影(交点 \((2,3)\) の\(x\)軸への影)となっています。

・正射影の面積

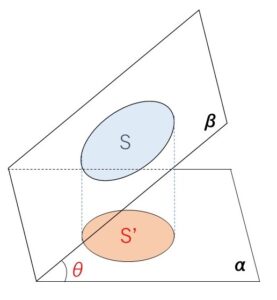
なす角が\(θ\) (\(0°≦θ≦90°\)) である、平面\(α,β\)があり、平面\(β\)上に面積が\(S\)である図形があるとします。この図形を平面\(α\)上へと正射影してできる図形の面積\(S’\)は

\(S’=Scosθ\)

となります。

(解説)

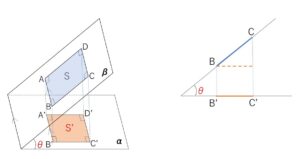
\(β\)上にある図形を、2辺が\(α,β\)の交線に平行である長方形とする。(残りの2辺は交線に垂直)

\(β\)上にある長方形を\(ABCD\)、\(α\)上の図形を四角形\(A’B’C’D’\)とすると、四角形\(A’B’C’D’\)も長方形となる。交線方向である、\(AB(CD)\)と\(A’B'(C’D’)\)の長さは変わらず、交線と垂直方向については、\(BC(AD)\)の \(\cosθ\) 倍 が\(B’C'(A’D’)\)となっているので、面積は

\(S’=Scosθ\)

他の図形、例えば曲線に囲まれた図形などについては微小な長方形に分割すれば同じ結論となる。

(例題)
\(xyz\)空間内の\(\vec{0}\)でないベクトル \(\vec{p}=(x,y,z)\) を考え、\(\vec{p’}=\displaystyle\frac{\vec{p}}{|\vec{p}|}\) とおく。

(1)\(\vec{p’}\)の大きさを求めよ。

(2)\(\vec{p}\)と\(x\)軸,\(y\)軸,\(z\)軸の正の向きとのなす角をそれぞれ\(α,β,γ\)とおくとき、
\(\vec{p’}=(\cosα,\cosβ,\cosγ)\) を示せ。

(3)\(\vec{p}=(3,4,12)\) とする。頂点\(O(0,0,0)\), \(A(a_1,a_2,a_3)\), \(B(b_1,b_2,b_3)\) の\(△OAB\)について、\(\vec{a}=(a_1,a_2,a_3)\), \(\vec{b}=(b_1,b_2,b_3)\) はともに\(\vec{p}\)に垂直とする。\(△OAB\)の面積を\(S\)とおくとき、\(xy\)平面上の点\(O\),\(A'(a_1,a_2,0)\), \(B'(b_1,b_2,0)\) が作る\(△OA’B’\)の面積を\(S\)を用いて表せ。

(解答)
(1)

\(|\vec{p’}|=\displaystyle\frac{|\vec{p}|}{|\vec{p}|}\)\(=1\)

(2)

\(\vec{p}=(x,y,z)\) と \(x\)軸の正方向 \(v_x=(1,0,0)\) とのなす角が\(α\)だから

\(\vec{p}\cdot\vec{v_x}=|\vec{p}||\vec{v_x}|\cosα\)
\(x=|\vec{p}|\cdot1\cdot\cosα\)
よって
\(\cosα=\displaystyle\frac{x}{|\vec{p}|}\)

同様に
\(\cosβ=\displaystyle\frac{y}{|\vec{p}|}\),　\(\cosγ=\displaystyle\frac{z}{|\vec{p}|}\)

したがって
\(\vec{p’}=\displaystyle\frac{\vec{p}}{|\vec{p}|}\)
\(=(\displaystyle\frac{x}{|\vec{p}|},\displaystyle\frac{y}{|\vec{p}|},\displaystyle\frac{z}{|\vec{p}|})\)
\(=(\cosα,\cosβ,\cosγ)\)

(3)

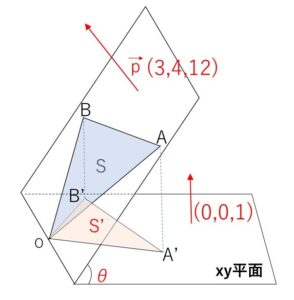
\(\vec{p}=(3,4,12)\)は、\(\vec{a},\vec{b}\)に垂直なので、平面\(OAB\)に垂直。
また、\(xy\)平面 (\(z=0\)) の法線ベクトルの1つは \(\vec{v_z}=(0,0,1)\)

\(\vec{p},\vec{v_z}\) のなす角を\(Φ\)とすれば
\(\vec{p}\cdot\vec{v_z}=|\vec{p}||\vec{v_z}|\cosΦ\)

\(12=\sqrt{3^2+4^2+12^2}\cdot1\cdot\cosΦ\)
よって
\(\cosΦ=\displaystyle\frac{12}{13}\)

平面\(OAB\)と\(xy\)平面のなす角を\(θ\)とすれば、\(\cosΦ>0\)より、\(θ=Φ\)で
\(\cosθ=\displaystyle\frac{12}{13}\)

\(△OAB\)の\(xy\)平面への正射影が\(△OA’B’\)なので

\(△OA’B’=△OAB\cosθ\)\(=\displaystyle\frac{12}{13}S\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→回転体(円錐面)の方程式　back→空間ベクトルの終点の存在範囲