倍数の和

等差数列の和の公式を利用して、倍数の和を求めていきます。

(例題1)
\(n\)を\(100\)以上\(600\)以下の整数とするとき、\(7\)で割ると\(2\)余る数\(n\)の総和を求めよ。

(解答)
\(n=7k+2\) (\(k\)は整数) とおけるので
\(100≦7k+2≦600\)
これを解くと
\(14≦k≦85.4\cdots\)

よって条件を満たす数を並べると
\(7×14+2,7×15+2,\cdots,7×85+2\)
つまり
\(100,107,\cdots,597\)

これは(公差\(7\)の)等差数列になり、
初項\(100\)、末項\(597\)、項数\(85-14\color{red}{+1}=72\) であるから総和\(S\)は

\(S=\displaystyle\frac{1}{2}\cdot72\cdot(100+597)\)\(=25092\)

(例題2)
\(1\)から\(1000\)までの自然数のうち、次のような数の総和をそれぞれ求めよ。
(1)\(2\)または\(3\)の倍数
(2)\(5\)の倍数でない数
(3)\(2\)または\(3\)または\(5\)の倍数
(4)\(2\)でも\(3\)でも\(5\)でも割り切れない数

(1)

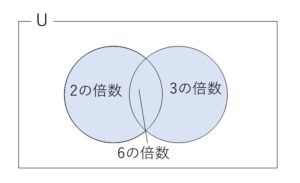
2の倍数を並べると
\(2×1,2×2,\cdots,2×500\)
よってその和\(S_2\)は
\(S_2=\displaystyle\frac{1}{2}\cdot500\cdot(2+1000)\)
\(=250500\)

3の倍数を並べると
\(3×1,3×2,\cdots,3×333\)
よってその和\(S_3\)は
\(S_3=\displaystyle\frac{1}{2}\cdot333\cdot(3+999)\)
\(=166833\)

6の倍数を並べると
\(6×1,6×2,\cdots,6×166\)
よってその和\(S_6\)は
\(S_6=\displaystyle\frac{1}{2}\cdot166\cdot(6+996)\)
\(=83166\)

したがって\(2\)または\(3\)の倍数の和は
\(S_2+S_3-S_6\)
\(=250500+166833-83166\)
\(=334167\)

(2)

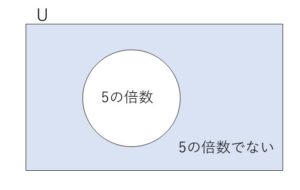
5の倍数を並べると
\(5×1,5×2,\cdots,5×200\)
よってその和\(S_5\)は
\(S_5=\displaystyle\frac{1}{2}\cdot200\cdot(5+1000)\)
\(=100500\)

\(1\)から\(1000\)までの自然数の和\(S\)は
\(S=\displaystyle\frac{1}{2}\cdot1000\cdot(1+1000)\)
\(=500500\)

したがって\(5\)の倍数でない数の和は
\(S-S_5\)
\(=400000\)

(3)

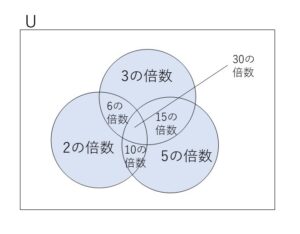
\(2,3,5,6\)の倍数の和は(1)(2)より
\(S_2=250500\)
\(S_3=166833\)
\(S_5=100500\)
\(S_6=83166\)

また、\(10,15,30\)の倍数を並べると
\(10×1,10×2,\cdots,10×100\)
\(15×1,15×2,\cdots,15×66\)
\(30×1,30×2,\cdots,30×33\)

となるから、それぞれの和\(S_{10},S_{15},S_{30}\)は
\(S_{10}=\displaystyle\frac{1}{2}\cdot100\cdot(10+1000)=50500\)
\(S_{15}=\displaystyle\frac{1}{2}\cdot66\cdot(15+990)=33165\)
\(S_{30}=\displaystyle\frac{1}{2}\cdot33\cdot(30+990)=16830\)

したがって、\(2\)または\(3\)または\(5\)の倍数の和は
\(S_2+S_3+S_5-(S_6+S_{10}+S_{15})+S_{30}\)
\(=250500+166833+100500-(83166+50500+33165)+16830\)
\(=367832\)

(4)

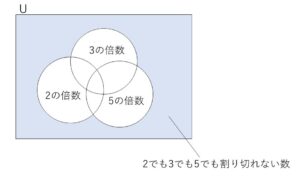
「\(2\)でも\(3\)でも\(5\)でも割り切れない数」ではない数は、「\(2\)の倍数または\(3\)の倍数または\(5\)の倍数」であるから、\(1\)から\(1000\)までの自然数の和\(S\)から(3)で求めた和を引けばよいので、求める数の和は

\(500500-367832\)\(=132668\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→2つの数列の共通項　back→等差数列の和