複利計算の例題に入る前に、単利と複利について整理していきます。
・単利と複利
銀行にお金を預けて一定期間が経過すると利息(利子)がつきお金が増えますが、この利息のつけ方には一般的には単利と複利(重利ともいう)という形式があります。
まず単利についてですが、これは最初の金額(元本(がんぽん)という)のみに利息がつき、期間経過で生まれた利息については利息がつかない形式です。
一方、複利は最初の金額だけでなく生まれた利息についても利息がつく形式です。
「最初の金額が1万円で、年利率(1年経過でつく利息の割合)\(5%\)」とした具体例でお金がどのように増えていくかを考えてみます。
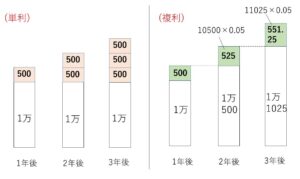
まず、単利については最初の元本1万円にしか利息がつかないので
1年後の合計 \(10000+500=10500\)
2年後の合計 \(10500+500=11000\)
3年後の合計 \(11000+500=11500\)
\(\cdots\)
というように、1年で\(10000\)円の\(5%\)である\(500\)円が加算されていくことになります。
一方複利については、1年後に\(10500\)円になるのは単利と同じですが、2年後にはこの\(10500\)円全体(元利合計)に利息が発生するので
1年後の合計 \(10000×1.05=10500\)
2年後の合計 \(10500×1.05=11025\) (\(10000×1.05^2\))
3年後の合計 \(11025×1.05=11576.25\) (\(10000×1.05^3\))
\(\cdots\)
という増え方になります。
この例からもわかるように単利については等差数列、複利については等比数列になっていることが分かります。
ちなみに基本的には銀行預金では複利形式がとられていて、単利の例は金銭の貸し借り(借金)などです。
(例題)
\(A\)氏は\(S\)円のマンションを\(n\)年の分割払い、年利率\(r(>0)\)で買うことにした。契約後\(1\)年たつごとに一定額\(a\)円ずつ払い、\(n\)年後に支払いを完了するものとする。1年ごとの複利計算として、以下の問に答えよ。
(1)\(a\)を\(S,n,r\)で表せ。
(2)\(a\)円の上限を百万円とし、年利率を\(5%\)とすると、支払い契約期間をどのように設定しても、2千万円以上のマンションを\(A\)氏は買うことができないことを示せ。
(解答)
(1)
\(k\)年後の残りの支払額を\(A_k\)とすると
\(A_1=S(1+r)-a\)
\(A_2=\{S(1+r)-a\}(1+r)-a\)
\(=S(1+r)^2-\{(1+r)+1\}a\)
\(A_3=[S(1+r)^2-\{(1+r)+1\}a](1+r)-a\)
\(=S(1+r)^3-\{(1+r)^2+(1+r)+1\}a\)
\(\cdots\) より
\(A_n=S(1+r)^n-\{(1+r)^{n-1}+(1+r)^{n-2}+\cdots+(1+r)+1\}a\)
(初項\(1\),公比\(1+r\),項数\(n\)の等比数列の和を考えて)
\(=S(1+r)^n-\displaystyle\frac{(1+r)^n-1}{(1+r)-1}\cdot a\)
\(=S(1+r)^n-\displaystyle\frac{(1+r)^n-1}{r}\cdot a\)
\(n\)年後に支払いが完了するので、\(A_n=0\) だから
\(\displaystyle\frac{(1+r)^n-1}{r}\cdot a=S(1+r)^n\)
したがって
\(a=\displaystyle\frac{Sr(1+r)^n}{(1+r)^n-1}\)
(2)
\(a=\displaystyle\frac{Sr(1+r)^n}{(1+r)^n-1}\) に、\(r=0.05\), \(S=2×10^{7}\)を代入して
\(a=\displaystyle\frac{10^6\cdot1.05^n}{1.05^n-1}\)
\(a≦10^6\) とすると
\(\displaystyle\frac{10^6\cdot1.05^n}{1.05^n-1}≦10^6\)・・・①
\(1.05^n≦1.05^n-1\)
この不等式を満たす自然数\(n\)は存在しないので、①を満たす自然数\(n\)は存在しない。
よって1年ごとの支払額の上限が百万円だと、返済が完了できない。
以上になります。お疲れさまでした。
ここまで見ていただきありがとうございました。
next→シグマ計算の基礎 back→対数と数列