階差数列について見ていきます。
・階差数列
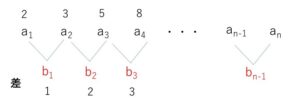
数列 \(a_n:2,3,5,8,12,\cdots\)
は、等差数列でも等比数列でもありませんが、隣同士の項の差をとると
\(3-2=1\), \(5-3=2\), \(8-5=3\), \(\cdots\) より
\(b_n:1,2,3,4,\cdots\)
と等差数列になっています。すると、\(a_1,a_2,a_3,\cdots\)を\(b_1,b_2,b_3,\cdots\)と\(a_1\)を用いて表すと
\(a_1=a_1\)
\(a_2=a_1+b_1\)
\(a_3=a_1+(b_1+b_2)\)
\(a_4=a_1+(b_1+b_2+b_3)\)
\(\cdots\)
となるので、\(a_n\)の一般項は
\(a_n=a_1+(b_1+b_2+b_3+\cdots+b_{n-1})\)
\(=a_1+\displaystyle\sum_{k=1}^{n-1}b_k\)・・・① (ただし\(n≧2\))
と表すことができます。\(n≧2\)の条件がつくのは、\(n=1\)のときシグマ記号が \(\displaystyle\sum_{k=1}^{0}\) となってしまうからです。
ここで、
\(b_1=a_2-a_1\)
\(b_2=a_3-a_2\)
\(b_3=a_4-a_3\)
\(\cdots\)
\(b_{n-1}=a_n-a_{n-1}\)
なので、\(b_n=a_{n+1}-a_{n}\) であり、\(a_n\)は①より次のように表すこともできます。
\(a_1=a_1+\displaystyle\sum_{k=1}^{n-1}(a_{k+1}-a_{k})\) (ただし\(n≧2\))
また、数列\(\{a_n\}\)に対して、\(b_n=a_{n+1}-a_{n}\) で定められる数列\(\{b_n\}\)を数列\(\{a_n\}\)の階差数列とよびます。
まず、階差数列は第\(n-1\)項までの和をとります。これは例えば\(a_4\)を求める際に、\(b_1+b_2+b_3\) と1つ少ない3つの和をとることからも分かります。
2つ目は、\(n≧2\) となることです。\(n=1\) のときは別途考えます。
なお、最初に挙げた数列
\(a_n:2,3,5,8,12,\cdots\)
の一般項を求めると、\(b_n=n\) より
\(a_n=a_1+\displaystyle\sum_{k=1}^{n-1}k\) (\(\displaystyle\sum k\) の公式で\(n→n-1\)とする)
\(=2+\displaystyle\frac{1}{2}(n-1)n\)
\(=\displaystyle\frac{1}{2}n^2-\displaystyle\frac{1}{2}n+2\) (\(n≧2\))
であり、\(n=1\) でも \(a_1=2\) となり成立するので
\(a_n=\displaystyle\frac{1}{2}n^2-\displaystyle\frac{1}{2}n+2\) (\(n=1,2,3\cdots\))
となります。
(例題1)
次の数列の一般項を求めよ。
\(a_n:1,3,7,15,31,63,\cdots\)
(解答)
\(a_n:1,3,7,15,31,63,\cdots\)
の階差数列を\(\{b_n\}\)とすると
\(b_n:2,4,8,16,32,\cdots\)
となるので、\(b_n=2^n\)。よって \(n≧2\) のとき
\(a_n=a_1+\displaystyle\sum_{k=1}^{n-1}2^{k}\)
(初項\(2\)、公比\(2\)、項数\(n-1\)の等比数列の和より)
\(=1+\displaystyle\frac{2(2^{n-1}-1)}{2-1}\)
\(=2^{n}-1\)・・・①
①で \(n=1\) とすると、\(2-1=1=a_1\) となるので、この式は\(n=1\)でも成立。
したがって
\(a_n=2^n-1\)
(例題2)
次の数列の一般項を求めよ。
(1)\(a_n:4,6,11,21,38,64,101,151,\cdots\)
(2)\(p_n:\displaystyle\frac{1}{6},\displaystyle\frac{1}{9},\displaystyle\frac{1}{14},\displaystyle\frac{1}{21},\displaystyle\frac{1}{30},\cdots\)
(解答)
(1)
\(b_n:2,5,10,17,26,37,50,\cdots\)
ですが、まだこの数列の規則性が分かりません。そこでさらに階差数列\(\{c_n\}\)を考えると
\(c_n:3,5,7,9,11,13,\cdots\)
となり、これは等差数列になっています。
\(a_n:4,6,11,21,38,64,101,151,\cdots\)
の階差数列\(\{b_n\}\)は
\(b_n:2,5,10,17,26,37,50,\cdots\)
であり、\(\{b_n\}\)の階差数列\(\{c_n\}\)は
\(c_n:3,5,7,9,11,13,\cdots\)
よって
\(c_n=3+2(n-1)=2n+1\) だから、\(n≧2\)のとき
\(b_n=b_1+\displaystyle\sum_{k=1}^{n-1}(2k+1)\) (シグマの部分は公式で\(n→n-1\)と置きかえます)
\(=2+\displaystyle\frac{2}{2}(n-1)n+(n-1)\)
\(=n^2+1\) (\(n=1\)でも成立)
ゆえに \(n≧2\) のとき
\(a_n=a_1+\displaystyle\sum_{k=1}^{n-1}(k^2+1)\) (同様に \(n→n-1\) と置きかえ)
\(=4+\displaystyle\frac{1}{6}(n-1)n\{2(n-1)+1\}+(n-1)\)
\(=4+\displaystyle\frac{1}{6}(n-1)n(2n-1)+(n-1)\)
\(=\displaystyle\frac{1}{3}n^3-\displaystyle\frac{1}{2}n^2+\displaystyle\frac{7}{6}n+3\) (\(n=1\)でも成立)
したがって
\(a_n=\displaystyle\frac{1}{3}n^3-\displaystyle\frac{1}{2}n^2+\displaystyle\frac{7}{6}n+3\)
(2)
について、そのまま階差数列をとってもうまくいきませんが、調和数列のように逆数をとると自然数の数列になるので、この階差数列を考えます。
\(\displaystyle\frac{1}{p_n}:6,9,14,21,30,\cdots\)
この数列\(\{\displaystyle\frac{1}{p_n}\}\)の階差数列\(\{r_n\}\)は
\(r_n:3,5,7,9\)
となるから
\(r_n=3+2(n-1)=2n+1\)
よって\(n≧2\)のとき
\(\displaystyle\frac{1}{p_n}=\displaystyle\frac{1}{p_1}+\displaystyle\sum_{k=1}^{n-1}(2k+1)\)
\(=6+\displaystyle\frac{2}{2}(n-1)n+(n-1)\)
\(=n^2+5\) (\(n=1\)でも成立)
したがって
\(p_n=\displaystyle\frac{1}{n^2+5}\)
以上になります。お疲れさまでした。
ここまで見ていただきありがとうございました。
next→部分分数分解① back→数列の和②(シグマ利用・シグマの中にシグマ)