ガウス記号を含む数列の和の例題です。
(例題1)
実数\(x\)に対し、\(x\)を超えない最大の整数を\([x]\)で表す。数列\(\{a_k\}\)を
\(a_k=[\sqrt{k}]\) (\(k=1,2,\cdots\))
で定義するとき、
\(S=\displaystyle\sum_{k=1}^{n^2}a_k\) (\(n\)は自然数)
を求めよ。
\(a_1=[\sqrt{1}]=1\), \(a_2=[\sqrt{2}]=1\), \(a_3=[\sqrt{3}]=1\)
\(a_4=[\sqrt{4}]=2\), \(a_5=[\sqrt{5}]=2\), \(a_6=[\sqrt{6}]=2\), \(a_7=[\sqrt{7}]=2\), \(a_8=[\sqrt{8}]=2\)
\(a_9=[\sqrt{9}]=3\), \(a_{10}=[\sqrt{10}]=3\)
・・・となり、\((1の群),(2の群),(3の群),\cdots\) という規則になっています。数値が変わるのは\(\sqrt{k}\)がちょうど整数となる\(1,4,9,\cdots\)(2乗で表せる)のときです。
(数列の末項が\(a_{n^2}\)という2乗の形になっていることにも着目)
群数列で考えると各群の項数が分かれば全体の和も分かるので、\([\sqrt{k}]=l\) (\(l\)は自然数) となるような\(k\)の範囲がどうなるかを求めていくことになります。例えば \([\sqrt{k}]=2\) では、\(2≦\sqrt{k}<3\) であればよいので \(4≦k<9\) であり、項数は\(k=4,5,6,7,8\) (\(9-4\)) の5項です(上の具体例と照らし合わせて下さい)。これを\(l\)として一般化するだけです。
(解答)
\(a_{n^2}=[\sqrt{n^2}]=n\) より
\(\{a_k\}:|1,1,1|2,2,2,2,2|3,\cdots|\cdots,n-1|n\)
項の値が \(n-1\) までは群数列で考えますが、\(n-1≧1\) となるように \(n≧2\) としておきます。
左から順に第\(1\)群、第\(2\)群、・・・第\(l\)群とすると、第\(l\)群の項の値はすべて\(l\)。
\(a_k=[\sqrt{k}]=l\) (\(l=1,2,\cdots,n-1\)) のとき (ただし\(n≧2\)とする)
\(l≦\sqrt{k}<(l+1)\) より
\(l^2≦k<(l+1)^2\)
よって第\(l\)群の項数は \((l+1)^2-l^2=2l+1\)
したがって、第\(l\)群には\(l\)が\(2l+1\)項並ぶから
\(S=\displaystyle\sum_{l=1}^{n-1}l(2l+1)+n\)
\(=\displaystyle\frac{2}{6}(n-1)n\{2(n-1)+1\}+\displaystyle\frac{1}{2}(n-1)n+n\)
\(=\displaystyle\frac{1}{3}(n-1)n(2n-1)+\displaystyle\frac{1}{2}(n-1)n+n\)
\(=\displaystyle\frac{1}{6}n\{2(n-1)(2n-1)+3(n-1)+6\}\)
\(=\displaystyle\frac{1}{6}n(4n^2-3n+5)\)
(\(n=1\) のとき \(S=a_{1^2}=[\sqrt{1}]=1\) だから、\(n=1\)のときも成立)
\(\cdots,l-1|l,l,\cdots,l|l+1,\cdots\)
となっていますが、ガウス記号表記に戻すと
\(\cdots,[\sqrt{l^2-1}]|[\sqrt{l^2}],[\sqrt{l^2+1}],\cdots,[\sqrt{(l+1)^2-1}]|[\sqrt{(l+1)^2}],\cdots\)
となっています。
(例題2)
自然数\(n\)に対して、\(\sqrt{n}\)に最も近い整数を\(a_{n}\)とする。
(1)\(m\)を自然数とするとき、\(a_n=m\) となる自然数\(n\)の個数を\(m\)を用いて表せ。
(2)\(\displaystyle\sum_{k=1}^{2001}a_k\) を求めよ。
最初のほうだけ具体例を挙げると
\(\sqrt{1},\sqrt{2}(1.41),\sqrt{3}(1.73),\sqrt{4},\sqrt{5}(2.23),\cdots\)
より、数列\(\{a_n\}\)は
\(1,1,2,2,2,\cdots\)
と、\((1の群),(2の群),(3の群),\cdots\) という群数列になります。この各群の個数を求めるのが(1)の誘導です。なお、\(2.5\)のような整数値の中間になるときは最も近い整数が\(2\)と\(3\)の2つ存在することになりますが、\(\sqrt{n}\)は整数か無理数にしかならないからあり得えないことは想像できます。(この2つ存在する場合がないことは解答を進めていくと途中で示すことができます)
(1)
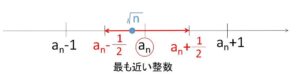
ガウス記号のときと同じように不等式評価をしていきます。
\(a_n\)は整数で、\(\sqrt{n}\)に最も近いものなので図より
\(a_n-\displaystyle\frac{1}{2}≦\sqrt{n}≦a_n+\displaystyle\frac{1}{2}\)
です。イコールがつくときは最も近い整数が2つ存在するときです。
\(a_n=m\) (\(m\)は自然数) より
\(m-\displaystyle\frac{1}{2}≦\sqrt{n}≦m+\displaystyle\frac{1}{2}\)
どの辺も正の値だから2乗して
\((m-\displaystyle\frac{1}{2})^2≦n≦(m+\displaystyle\frac{1}{2})^2\)
よって
\(m^2-m+\displaystyle\frac{1}{4}≦n≦m^2+m+\displaystyle\frac{1}{4}\)・・・①
また、この不等式を満たす\(n\)は、\(\displaystyle\frac{1}{4}=0.25\) なので
\(n=m^2-m+1,m^2-m+2,\cdots,m^2+m\)
です。
\(m,n\)は自然数だから①の等号が成り立つことはないので、最も近い整数は各\(n\)につき1つずつ。また①を満たす\(n\)は
\(n=m^2-m+1,m^2-m+2,\cdots,m^2+m\)
だから、\(a_n=m\) となる\(n\)の個数は
\((m^2+m)-(m^2-m+1)+1\)
\(=2m\)(個)
(2)
\(1,1|2,2,2,2|3,3,3,3,3,3|\cdots|m,m,\cdots,m\ (2m個)|\cdots\)
という群数列です。左から順に第\(1\)群、第\(2\)群、・・・として、\(a_{2001}\)がまず第何群にあるかを調べます。
(1)よりこの数列は
\(1,1|2,2,2,2|3,3,3,3,3,3|\cdots\)
で、同じ数の部分を群とみて左から順に第\(1\)群、第\(2\)群・・・とすると、第\(m\)群には数\(m\)が\(2m\)個並ぶ。
初めから\(m\)群の最後の項までの項数は
\(2+4+6+\cdots+2m\)
\(=\displaystyle\frac{1}{2}m(2m+2)\)
\(=m(m+1)\)
だから、\(a_{2001}\)が第\(m\)群にあるとすると、
\((m-1)m<2001≦m(m+1)\)
であり、この不等式を満たす\(m\)は\(m=45\)
よって\(a_{2001}\)は第\(45\)群にあり、その値は\(45\)。
第\(44\)群の最後の項までの項数は
\(44\cdot45=1980\)
だから、\(2001-1980=21\) より \(a_{2001}\)は第\(45\)群の第\(21\)項。
\(44\)群までは群全部の和をとって、\(45\)群については\(21\)個だけ和をとります。( \(a_{2001}\)は\(45\)群の途中にある)
したがって第\(m\)群には数\(m\)が\(2m\)個並ぶことから
\(\displaystyle\sum_{k=1}^{2001}a_k\)
\(=\displaystyle\sum_{m=1}^{44}m\cdot2m+45×21\)
\(=\displaystyle\sum_{m=1}^{44}2m^2+945\)
\(=\displaystyle\frac{2}{6}\cdot44\cdot45\cdot89+945\)
\(=59685\)
以上になります。お疲れさまでした。
ここまで見ていただきありがとうございました。
next→等差・等比・階差の漸化式 back→絶対値の和