やや発展的な帰納法を利用する問題について見ていきます。
(例題1)
(1)\(a_1\cdot a_2\cdot\cdots\cdot a_n=1\) である任意の\(n\)個 (\(n≧2\)) の正の数\(a_1,a_2,\cdots,a_n\)に対して、\(a_1+a_2+\cdots+a_n≧n\) が成り立つことを示せ。
(2)\(n\)個 (\(n≧2\)) の正の数\(a_1,a_2,\cdots,a_n\)に対して
\(\displaystyle\frac{a_1+a_2+\cdots+a_n}{n}≧\sqrt[n]{a_1a_2\cdots a_n}\)
が成り立つことを示せ。
(解答)
(1)
数学的帰納法で証明していきますが、\(k→k+1\) のときに少し工夫が必要です。
またスタートは\(n=2\)からです。
「\(n\)個の正の数の積が\(1\)であるとき、それらの和は\(n\)以上」・・・①
を数学的帰納法で示す。
[1]\(n=2\)のとき
\(a_1a_2=1\)
このとき相加相乗平均の不等式より
\(a_1+a_2≧2\sqrt{a_1a_2}\)
\(a_1+a_2≧2\)
よって、①は\(n=2\)のとき成り立つ。
[2]\(n=k\)のとき (\(k=2,3,\cdots\))
①が成り立つと仮定する。
「\(a_1\cdot a_2\cdot\cdots\cdot a_{k}\cdot a_{k+1}=1\) のとき、\(a_1+a_2+\cdots+a_k+a_{k+1}≧k+1\)」ですが、①を言葉で考えたのは、\(n=k\) の仮定を 「\(a_1\cdot a_2\cdot\cdots\cdot a_{k}=1\)」としてしまうと、\(a_{k+1}=1\) (に限る)という限定的な結論になってしまうことを避けるためです(\(k+1\)個の数は任意でなくてはならないのでダメ)。問題文の意味することは、個々の\(n=□\)について「\(n\)個の正の数の積が\(1\)のときそれら\(n\)個の数の和が\(n\)以上」です。
ここで\(k+1\)個の正の数、\(a_1,a_2,\cdots,a_k,a_{k+1}\) について、積の条件から
\(a_1a_2\cdots\cdot a_{k}a_{k+1}=1\)
\(a_1,a_2,\cdots,a_{k-1},a_{k}a_{k+1}\) は\(k\)個の正の数で、その積は\(1\)だから
\(n=k\)の仮定から
\(a_1+a_2+\cdots+a_{k-1}+a_{k}a_{k+1}≧k\)
両辺に\(1\)を加えて
\(a_1+a_2+\cdots+a_{k-1}+a_{k}a_{k+1}+1≧k+1\)・・・②
\(a_1+a_2+\cdots+a_{k-1}+a_k+a_{k+1}≧k+1\)
と比べると、\(a_k+a_{k+1}≧a_{k}a_{k+1}+1\) が示せればよいことが分かります。これを整理して因数分解すると、\((a_{k}-1)(1-a_{k+1})≧0\)・・・③ですが、ここでこの例題では、登場する正の数の順番を入れ替えても問題ない(対称性がある)から、\(a_1,a_2,\cdots,a_{k-1},a_{k},a_{k+1}\)の数の大小を設定することで、③を示すことができます。
\(a_1,a_2,\cdots,a_k,a_{k+1}\) について
最大の数を\(a_k\)、最小の数を\(a_{k+1}\)
としても一般性を失わず、これらの積が\(1\)であることから
\(a_k≧1\), \(a_{k+1}≦1\)
よって
\(a_k+a_{k+1}-(a_{k}a_{k+1}+1)\)
\(=(a_k-1)(1-a_{k+1})≧0\)
だから
\(a_k+a_{k+1}≧a_{k}a_{k+1}+1\)・・・③
したがって②③より
\(a_1+a_2+\cdots+a_{k-1}+a_{k}+a_{k+1}≧k+1\)
となるから、\(n=k+1\)でも①は成立する。
[1][2]より\(2\)以上の自然数について題意は成立する。
(参考)等号成立について
等号成立は \(a_1=a_2=\cdots=a_n=1\) ですが、これも帰納法によって証明できます。概略をいうと
[1]\(n=2\)のとき
相加相乗平均の不等式の等号が成り立つときなので、\(a_1=a_2\)
これと\(a_1a_2=1\) から、\(a_1=a_2=1\)
[2]\(n=k\)のとき
\(a_1+a_2+\cdots+a_{k-1}+a_{k}a_{k+1}+1≧k+1\)・・・②
の等号が成り立つのは\(n=k\)での等号成立の仮定より
\(a_1=a_2=\cdots=a_{k-1}=a_{k}a_{k+1}=1\)・・・(i)
\(a_k+a_{k+1}≧a_{k}a_{k+1}+1\)・・・③
の等号が成り立つのは因数分解した式から
\(a_{k}=1\) または \(a_{k+1}=1\)・・・(ii)
\(n=k+1\)の不等式
\(a_1+a_2+\cdots+a_{k-1}+a_{k}+a_{k+1}≧k+1\)
が成り立つのは、②③の両方の等号が成り立つときだからその条件は(i)かつ(ii)
したがって\(n=k+1\)の等号成立条件は
\(a_1=a_2=\cdots=a_k=a_{k+1}=1\)
と結論づけることができます。
(2)
\(\displaystyle\frac{a_1}{\sqrt[n]{a_1a_2\cdots a_n}}+\displaystyle\frac{a_2}{\sqrt[n]{a_1a_2\cdots a_n}}+\cdots+\displaystyle\frac{a_n}{\sqrt[n]{a_1a_2\cdots a_n}}≧n\)
ですが、左辺の項をすべて掛けると1になるので(1)の結果が使えます。
\(n\)個の正の数
\(\displaystyle\frac{a_1}{\sqrt[n]{a_1a_2\cdots a_n}},\displaystyle\frac{a_2}{\sqrt[n]{a_1a_2\cdots a_n}},\cdots,\displaystyle\frac{a_n}{\sqrt[n]{a_1a_2\cdots a_n}}\)
について、これらの積は\(1\)だから(1)より
\(\displaystyle\frac{a_1}{\sqrt[n]{a_1a_2\cdots a_n}}+\displaystyle\frac{a_2}{\sqrt[n]{a_1a_2\cdots a_n}}+\cdots+\displaystyle\frac{a_n}{\sqrt[n]{a_1a_2\cdots a_n}}≧n\)
したがって
\(\displaystyle\frac{a_1+a_2+\cdots+a_n}{n}≧\sqrt[n]{a_1a_2\cdots a_n}\)
(参考)
等号は(1)の参考から
\(\displaystyle\frac{a_1}{\sqrt[n]{a_1a_2\cdots a_n}}=\displaystyle\frac{a_2}{\sqrt[n]{a_1a_2\cdots a_n}}=\cdots=\displaystyle\frac{a_n}{\sqrt[n]{a_1a_2\cdots a_n}}=1\)
より
\(a_1=a_2=\cdots=a_n\)
となります。\(=1\)については、\(a_i=\sqrt[n]{a_1a_2\cdots a_n}\) (\(i=1,2,\cdots,n\))ですが、これは \(a_1=a_2=\cdots=a_n\) から成り立つので省きます。
なお(2)の不等式は\(n\)変数の相加相乗平均の不等式といわれるもので、2つの数の相加相乗平均の不等式を一般化したものです。
(例題2)
関数\(f(x)\)は、\(p+q=1\) を満たすすべての正の数\(p,q\)と、すべての実数\(x,y\)に対して、
\(f(px+qy)≦pf(x)+qf(y)\) を満たしているとする。
このとき、\(2\)以上の自然数\(n\)について、\(p_1+p_2+\cdots+p_n=1\) を満たすすべての正の数\(p_1,p_2,\cdots,p_n\)と、すべての実数\(x_1,x_2,\cdots,x_n\)に対して
\(f(p_1x_1+p_2x_2+\cdots+p_nx_n)≦p_1f(x_1)+p_2f(x_2)+\cdots+p_nf(x_n)\)
が成り立つことを証明せよ。
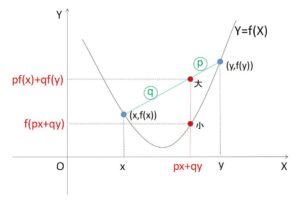
\(x<y\)のとき、\(p+q=1\) より \(px+qy=\displaystyle\frac{px+qy}{p+q}\) なので、\((px+qy,0)\) は 2点 \((x,0),(y,0)\) を\(q:p\) の比に内分する点の座標で、 \(pf(x)+qf(y)\) も同様なので、\(f(px+qy)≦pf(x)+qf(y)\) は「\(x\)座標が\(px+qy\)のときの関数の値は、2点 \((x,f(x)),(y,f(y))\) を\(q:p\) の比に内分する点の\(y\)座標より小さい」ということを表しています。よって図より関数\(f(x)\)は下に凸であることになります。不等号が逆だと上に凸の関数となり、このグラフの凸性を表す不等式は凸不等式とよばれます。
(解答)
命題\(A(n):\)「\(p_1+p_2+\cdots+p_n=1\)のとき、\(f(p_1x_1+p_2x_2+\cdots+p_nx_n)≦p_1f(x_1)+p_2f(x_2)+\cdots+p_nf(x_n)\)
が成り立つ」
ことを数学的帰納法で示す。
与条件は「\(p+q=1\) を満たすすべての正の数\(p,q\)と、すべての実数\(x,y\)に対して、
\(f(px+qy)≦pf(x)+qf(y)\)」・・・①
であり
[1]\(n=2\) のとき
\(p_1+p_2=1\) だから①より
\(f(p_1x_1+p_2x_2)≦p_1f(x_1)+p_2f(x_2)\)
が成り立つので、\(A(2)\)は正しい。
[2]\(n=k\) のとき (\(k=2,3,\cdots\))
命題\(A(k)\)が正しいと仮定する。
命題\(A(k+1)\)の条件より
\(p_1+p_2+\cdots+p_{k-1}+(p_k+p_{k+1})=1\)
(まず帰納法の仮定が使えるように\(k\)個の和になるようにします)
\(p_k+p_{k+1}=P\) とおくと
\(p_1+p_2+\cdots+p_{k-1}+P=1\)・・・②
\(p_1+p_2+\cdots+p_n=1\)のとき、
\(f(p_1x_1+p_2x_2+\cdots+p_kx_k+p_{k+1}x_{k+1})\)
\(≦p_1f(x_1)+p_2f(x_2)+\cdots+p_kf(x_k)+p_{k+1}f(x_{k+1})\)
なので、この左辺になるように、\(PX=p_kx_{k}+p_{k+1}x_{k+1}\) となる\(X\)を決定します。
②から\(n=k\)の仮定より
\(f(p_1x_1+p_2x_2+\cdots+p_{k-1}x_{k-1}+PX)\)
\(≦p_1f(x_1)+p_2f(x_2)+\cdots+p_{k-1}f(x_{k-1})+Pf(X)\)・・・③
であり、
\(X=\displaystyle\frac{p_kx_{k}+p_{k+1}x_{k+1}}{P}=\displaystyle\frac{p_kx_{k}+p_{k+1}x_{k+1}}{p_k+p_{k+1}}\)
とすれば③は
\(f(p_1x_1+p_2x_2+\cdots+p_{k-1}x_{k-1}+p_kx_{k}+p_{k+1}x_{k+1})\)
\(≦p_1f(x_1)+p_2f(x_2)+\cdots+p_{k-1}f(x_{k-1})\)
\(+(p_k+p_{k+1})f(\displaystyle\frac{p_k}{p_k+p_{k+1}}x_k+\displaystyle\frac{p_{k+1}}{p_k+p_{k+1}}x_{k+1})\)・・・④
また、
\(\displaystyle\frac{p_k}{p_k+p_{k+1}}+\displaystyle\frac{p_{k+1}}{p_k+p_{k+1}}=1\)
だから、[1]より
\(f(\displaystyle\frac{p_k}{p_k+p_{k+1}}x_k+\displaystyle\frac{p_{k+1}}{p_k+p_{k+1}}x_{k+1})≦\displaystyle\frac{p_k}{p_k+p_{k+1}}f(x_k)+\displaystyle\frac{p_{k+1}}{p_k+p_{k+1}}f(x_{k+1})\)
したがってこれと④より
\(f(p_1x_1+p_2x_2+\cdots+p_{k-1}x_{k-1}+p_kx_{k}+p_{k+1}x_{k+1})\)
\(≦p_1f(x_1)+p_2f(x_2)+\cdots+p_{k-1}f(x_{k-1})+p_kf(x_k)+p_{k+1}f(x_{k+1})\)
が成り立つから、\(A(k+1)\)も正しい。
[1][2]より\(2\)以上の自然数について\(A(n)\)は正しいから題意は示された。
以上になります。お疲れさまでした。
ここまで見ていただきありがとうございました。
next→図形と数列・漸化式① back→一般項の予想と帰納法、n≦k の仮定