図形的要素を含んだ分数関数に関する例題です。
(例題)
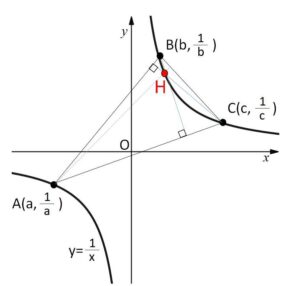
\(xy\)平面の双曲線 \(y=\displaystyle\frac{1}{x}\) 上の相異なる3点を\(A,B,C\)とし、その\(x\)座標を、それぞれ\(a,b,c\)とする。このとき、次の各問に答えよ。
(1)直線\(AB\)に垂直な直線の傾きは ( ア ) である。\(△ABC\)の垂心を\(H\)とするとき、\(H\)の\(x,y\)座標を\(a,b,c\)を用いて表すと、\(x=\)( イ )、\(y=\)( ウ ) である。よって、\(A,B,C\)が双曲線上を動くとき、\(H\)の軌跡は\(x,y\)の関係式 ( エ ) で表され、\(H\)はこの関係式で表される図形上のすべての点を動く。
(2)\(△ABC\)の外心を\(P(x,y)\)とする。
(i)\(P\)の座標\(x,y\)を、\(a,b,c\)を用いて表せ。
(ii)\(a,b,c\)が \(a+b=0\), \(c=1\) を満たすとき、\(P(x,y)\)の軌跡を求め、図示せよ。
(解答)
(1)
なお、三角形の各頂点から対辺に垂線をひくと、3つの垂線は1点(垂心)で交わります。よって解答では2本の垂線のみで交点を考えていくことにします。
\(a,b,c\)は\(0\)でなく、相異なることに注意する。
(ア)
直線\(AB\)の傾きは
\(\displaystyle\frac{\displaystyle\frac{1}{b}-\displaystyle\frac{1}{a}}{b-a}=\displaystyle\frac{a-b}{ab(b-a)}=-\displaystyle\frac{1}{ab}\)
よってこれに垂直な直線の傾きは
\(ab\)
(イ)(ウ)
直線\(CH\)の方程式は(ア)より
\(y=ab(x-c)+\displaystyle\frac{1}{c}\)・・・①
また、(ア)と同様に直線\(AC\)の傾きを求めると \(-\displaystyle\frac{1}{ca}\) だから、直線\(BH\)の方程式は
\(y=ca(x-b)+\displaystyle\frac{1}{b}\)・・・②
①と②の交点が\(H\)だから連立してその座標を求めると
①-②より
\(0=a(b-c)x+\displaystyle\frac{b-c}{bc}\)
よって
\(x=-\displaystyle\frac{1}{abc}\)
これを①に代入して
\(y=-abc\)
(エ)
(ウ)より、積\(abc\)を消去して
\(y=\displaystyle\frac{1}{x}\)
積\(abc\)は\(0\)以外の値をとりうるので\(H\)はこの曲線上全体を動く。
なお(エ)の結果から垂心はもともとの曲線上を動くことになります。
(2)
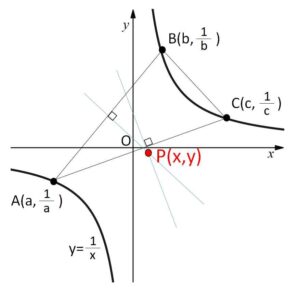
(i)
線分\(AB\)の垂直2等分線の方程式は(1)より傾きが\(ab\)だから
\(y=ab(x-\displaystyle\frac{a+b}{2})+\displaystyle\frac{1}{2}(\displaystyle\frac{1}{a}+\displaystyle\frac{1}{b})\)・・・③
線分\(AC\)の垂直2等分線の方程式は(1)より傾きが\(ca\)だから
\(y=ca(x-\displaystyle\frac{c+a}{2})+\displaystyle\frac{1}{2}(\displaystyle\frac{1}{c}+\displaystyle\frac{1}{a})\)・・・④
③④の交点が\(P\)だから、その座標を求めると
③-④より
\(0=a(b-c)x-\displaystyle\frac{ab(a+b)}{2}+\displaystyle\frac{ca(c+a)}{2}+\displaystyle\frac{c-b}{2bc}\)
\(a(c-b)x=\displaystyle\frac{a}{2}(-ab-b^2+c^2+ca)+\displaystyle\frac{c-b}{2bc}\)
\(a(c-b)x=\displaystyle\frac{a}{2}\{(c-b)(c+b)+a(c-b)\}+\displaystyle\frac{c-b}{2bc}\)
\(a(c-b)x=\displaystyle\frac{a(c-b)}{2}(a+b+c)+\displaystyle\frac{c-b}{2bc}\)
よって
\(x=\displaystyle\frac{1}{2}(a+b+c+\displaystyle\frac{1}{abc})\)
これを③に代入して
\(y=ab(\displaystyle\frac{1}{2}c+\displaystyle\frac{1}{2abc})+\displaystyle\frac{1}{2}(\displaystyle\frac{1}{a}+\displaystyle\frac{1}{b})\)
よって
\(y=\displaystyle\frac{1}{2}(abc+\displaystyle\frac{1}{a}+\displaystyle\frac{1}{b}+\displaystyle\frac{1}{c})\)
(ii)
\(c=1\) より、\(a≠1\) かつ \(b≠1\)
\(a+b=0\) より、\(b=-a\) だから \(a≠-1\)
また、\(a≠0\) のとき \(b≠0\)
よって \(a≠0,±1\) のとき、\(a,b,c\)は相異なり、\(0\)でない。
(i)の\(x,y\)に、\(c=1\), \(b=-a\) を代入して
\(x=\displaystyle\frac{1}{2}(1-\displaystyle\frac{1}{a^2})\)・・・⑤
\(y=\displaystyle\frac{1}{2}(-a^2+1)\)・・・⑥
⑤と\(a≠0,±1\) より
\(x<\displaystyle\frac{1}{2}\), \(x≠0\)・・・⑦
また⑤⑥より
\(x-\displaystyle\frac{1}{2}=-\displaystyle\frac{1}{2a^2}\)
\(y-\displaystyle\frac{1}{2}=-\displaystyle\frac{1}{2}a^2\)
\(a^2\)を消去して
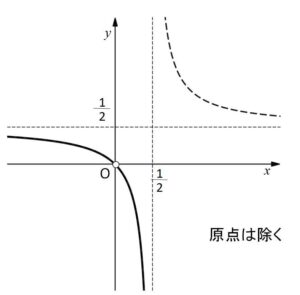
\((x-\displaystyle\frac{1}{2})(y-\displaystyle\frac{1}{2})=\displaystyle\frac{1}{4}\)
この方程式で表されるグラフは、\(xy=\displaystyle\frac{1}{4}\) を \(x\)軸方向に\(\displaystyle\frac{1}{2}\)、\(y\)軸方向に\(\displaystyle\frac{1}{2}\) に平行移動したもので、⑦の範囲で図示すると次の通り。
以上になります。お疲れさまでした。
ここまで見ていただきありがとうございました。
next→2次式の分数関数 back→分数方程式・不等式とグラフの共有点②