前回は 2次式の判別式\(D>0\) の2次不等式の解法について触れましたが、今回は判別式が0や負の値になるときの2次不等式について考えていきます。
(判別式\(D=0\)の場合)
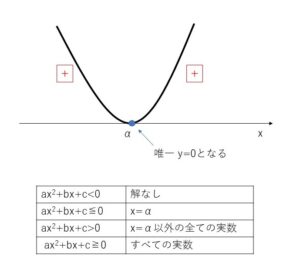
\(y=ax^2+bx+c\) (\(a>0\) \(b^2-4ac=0\))のグラフは、\(x\)軸とただ1つの共有点をもち、その\(x\)座標を\(α\)とおくと、次のようになります。
\(ax^2+bx+c<0\)の解は、グラフより\(y=ax^2+bx+c\)が負の値をとらないことから、存在しません。
\(ax^2+bx+c>0\)の解は、\(x=α\)のとき\(y=ax^2+bx+c=0\)となる以外、他の\(x\)ではすべて正の値をとるので、\(x=α\)以外の全ての実数となります。
続いて不等号にイコールが付いた場合ですが、
\(ax^2+bx+c≦0\)の解は、\(x=α\)のとき\(y=ax^2+bx+c=0\)となる以外、他の\(x\)ではすべて正の値をとるので、解は\(x=α\)のみです。
\(ax^2+bx+c≧0\)の解は、グラフよりすべての実数となります。
\(a<0\)の場合は、上に凸のグラフとして考えるか、両辺に\(-1\)をかけて\(a>0\)場合に帰着させます。ただし、マイナスの数をかけると不等号の向きが入れ替わることに注意してください。
(判別式\(D<0\)の場合)
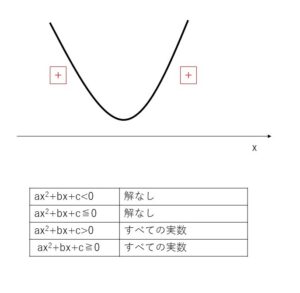
\(y=ax^2+bx+c\) (\(a>0\) \(b^2-4ac<0\))のグラフは、x軸と共有点を持たず常に\(y\)の値が正となります。
\(ax^2+bx+c<0\)の解は、グラフより\(y=ax^2+bx+c\)が負の値をとらないことから、存在しません。
\(ax^2+bx+c>0\)の解は、グラフよりすべての実数となります。
続いて不等号にイコールが付いた場合ですが、
\(ax^2+bx+c≦0\)の解は、\(y\)は常に正の値をとるため、存在しません。
\(ax^2+bx+c≧0\)の解は、グラフよりすべての実数となります。
\(a<0\)の場合は、上に凸のグラフとして考えるか、両辺に\(-1\)をかけて\(a>0\)場合に帰着させます。
(例題)次の不等式を解け。
(1)\(x^2-2x+1>0\)
(2)\(2x^2+4x+3≧0\)
(3)\(4x^2-4x+1<0\)
(4)\(-2x^2-7x-7≧0\)
(解答)
(1)\(D=4-4=0\) で
与式は \((x-1)^2>0\)
よって解は \(x=1\) 以外の全ての実数
(2)\(D=16-24<0\) から
\(y=2x^2+4x+3\)は常に正の値をとる
よって 解は全ての実数
与式は \((2x-1)^2<0\)
よって 解はなし
\(2x^2+7x+7\)\(≦\)\(0\)
\(D=49-56<0\)より
\(y=2x^2+7x+7\) は常に正の値をとる
よって解はなし
以上になります。お疲れ様でした。
ここまで読んで頂きありがとうございました。