今回からは2次不等式について学んでいきます。2次関数のグラフとx軸の位置関係を活用していきます。
・2次不等式の解き方
\(ax^2+bx+c<0\) (ただし\(a≠0\))などの2次式の不等式を、2次不等式とよびます。2次不等式を解くときは2次関数のグラフを活用します。まずは左辺を \(y=ax^2+bx+c\) とおいたとき、このグラフが\(x\)軸と2点で交わるとき(つまり \(ax^2+bx+c=0\) の判別式が正の値)から考えていきます。
(判別式\(D>0\)の場合)
\(y=ax^2+bx+c\) (ただし \(a≠0\) \(b^2-4ac>0\)) のグラフで、まずは \(a>0\) の場合を考えます。交点の\(x\)座標をあらわすため、\(ax^2+bx+c=0\)の2解を\(α,β\)(\(α<β\))とおくとグラフは次のようになります。ここで \(ax^2+bx+c<0\) の解は左辺が負の値のなるときの\(x\)、つまり\(y=ax^2+bx+c\) が負の値をとる\(x\)の範囲なので(グラフが\(x\)軸より下側の部分の範囲)、グラフより、\(α<x<β\)となります。同様に考えると、\(ax^2+bx+c>0\)は \(y=ax^2+bx+c\) が正の値をとる\(x\)の範囲なので(グラフが\(x\)軸より上側の部分の範囲) \(x<α\) または \(x>β\) となります。不等号にイコールがついていても同じなのでまとめると次のようになります。
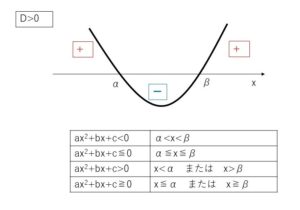
このとき\(y=ax^2+bx+c\)は、\(x=α,β\) のとき\(y=0\)となるので、グラフは\((α,0)\)と\((β,0)\)の2点で\(x\)軸と交わります。
\(a<0\)の場合は上に凸のグラフとして考えるか、不等式の両辺に\(-1\)をかけることで\(a>0\)の場合に帰着させます。ただしマイナスの数をかけると不等号の向きが入れ替わることに注意してください。
(例題)次の不等式を解け。
(1)\(x^2-3x+2≦0\)
(2)\(-x^2+3x+2<0\)
(解答)
(1)因数分解すると
\((x-1)(x-2)≦0\)
グラフより、解は
\(1≦x≦2\)
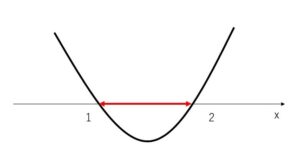
(2)両辺\(-1\)をかけて
\(x^2-3x-2\)\(>\)\(0\)
\(x^2-3x-2=0\)の解は
\(x=\displaystyle\frac{3±\sqrt{17}}{2}\) なので
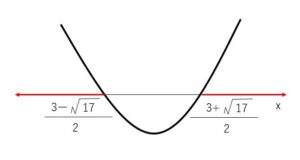
グラフより解は
\(x<\displaystyle\frac{3-\sqrt{17}}{2}\)、\(x>\displaystyle\frac{3+\sqrt{17}}{2}\)
以上になります。お疲れさまでした。
ここまで読んで頂きありがとうございました。