平均値の定理(c,θの具体例)

これから平均値の定理に関する例題を扱っていきますが、まずはイメージをつかむために、具体的に\(c\)や\(θ\)を求める例題を扱います。

(例題1)
次の関数\(f(x)\)と区間について、平均値の定理の条件を満たす\(c\)の値を求めよ。

(平均値の定理)
\(\displaystyle\frac{f(b)-f(a)}{b-a}=f'(c)\)、\(a<c<b\)

(1)\(f(x)=e^{x}\)　\([0,1]\)
(2)\(f(x)=x^4\)　\([a,b]\)

(解答)
(1)(2)ともに区間内で微分可能(連続でもある)だから、平均値の定理が利用できる。

(1)

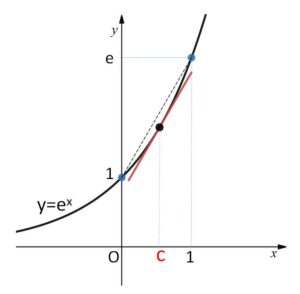
\(f(x)=e^{x}\)   より
\(f'(x)=e^{x}\)

よって区間\([0,1]\)において平均値の定理から
\(\displaystyle\frac{e^1-e^0}{1-0}=e^c\)、\(0<c<1\)
ゆえに
\(e^{c}=e-1\)
\(c=\log(e-1)\)　(\(0<c<1\) を満たす)

(2)
\(f(x)=x^4\)   より
\(f'(x)=4x^3\)

よって区間\([a,b]\)において平均値の定理から
\(\displaystyle\frac{b^4-a^4}{b-a}=4c^3\)、\(a<c<b\)
ゆえに
\(c^3=\displaystyle\frac{(b^2+a^2)(b+a)}{4}\)

\(c=\sqrt[3]{\displaystyle\frac{(b^2+a^2)(b+a)}{4}}\)　(\(a<c<b\)を満たす)

(例題2)
\(f(x)=x^3\) のとき
\(f(a+h)-f(a)=hf'(a+θh)\)、\(0<θ<1\)
を満たす\(θ\)を求めよ。また、\(\displaystyle\lim_{h \to +0}θ\) を求めよ。ただし、\(h,a\)は正の数とする。

(解答)
\(f(x)=x^3\) のとき
\(f'(x)=3x^2\)

与式より
\((a+h)^3-a^3=h\cdot3(a+θh)^2\)

\(h,a,θ\)が正の数であることに注意して
\(3a^2+3ah+h^2=3(a+θh)^2\)
\(\sqrt{3}(a+θh)=\sqrt{3a^2+3ah+h^2}\)
\(\sqrt{3}θh=\sqrt{3a^2+3ah+h^2}-\sqrt{3}a\)

したがって
\(θ=\displaystyle\frac{\sqrt{3a^2+3ah+h^2}-\sqrt{3}a}{\sqrt{3}h}\)

また
\(\displaystyle\lim_{h \to +0}θ=\displaystyle\lim_{h \to +0}\displaystyle\frac{\sqrt{3a^2+3ah+h^2}-\sqrt{3}a}{\sqrt{3}h}\)

(有理化して)

\(=\displaystyle\lim_{h \to +0}\displaystyle\frac{(3a^2+3ah+h^2)-3a^2}{\sqrt{3}h(\sqrt{3a^2+3ah+h^2}+\sqrt{3}a)}\)

\(=\displaystyle\lim_{h \to +0}\displaystyle\frac{3a+h}{\sqrt{3}(\sqrt{3a^2+3ah+h^2}+\sqrt{3}a)}\)

\(=\displaystyle\frac{3a}{\sqrt{3}(\sqrt{3a^2}+\sqrt{3}a)}\)

\(=\displaystyle\frac{1}{2}\)

以上になります。お疲れ様でした。
ここまで見ていただきありがとうございました。
next→平均値の定理と不等式の証明　back→ロルの定理と平均値の定理