微分を利用する図形問題です。
(例題1)
図のように幅\(4\)のテープを端点\(C\)が対辺に重なるように折るとき、三角形\(ABC\)の面積が最小になるような\(θ\)とそのときの面積を求めよ。
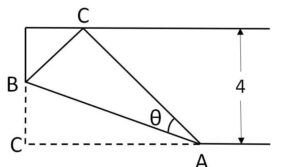
元に戻すとイメージしやすいですが、折り返しているので、2つの直角三角形\(ABC\)は合同です。
\(AC\)の長さを\(θ\)で表すことができれば、
\(△ABC=\displaystyle\frac{1}{2}AC\cdot CB=\displaystyle\frac{1}{2}AC\cdot AC\tanθ\)
より、面積を\(θ\)で表すことができます。
\(\angle CAC=2θ\) を利用すると、\(AC\)が楽に求まります。
(解答)
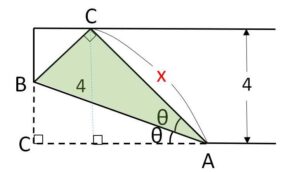
\(AC=x\) とおく。
図より
\(x\sin2θ=4\) より
\(x=\displaystyle\frac{4}{\sin2θ}\)
したがって
\(△ABC=\displaystyle\frac{1}{2}AC\cdot CB\)
\(=\displaystyle\frac{1}{2}AC^2\tanθ\)
\(=\displaystyle\frac{1}{2}x^2\tanθ\)
\(=\displaystyle\frac{1}{2}\cdot\displaystyle\frac{16}{\sin^22θ}\cdot\tanθ\)
(後々のために変形して\(\sinθ,\cosθ\)のみで表しておくと)
\(=\displaystyle\frac{8}{4\sin^2θ\cos^2θ}\cdot\displaystyle\frac{\sinθ}{\cosθ}\)
\(=\displaystyle\frac{2}{\sinθ\cos^3θ}\)
\(θ\)の範囲ですが、テープをちょうど2つ折りにすると \(2θ=0\)。また、\(C\)が\(A\)の真上にくるように折ると \(2θ=\displaystyle\frac{π}{2}\) です。これが範囲のぎりぎりになります。
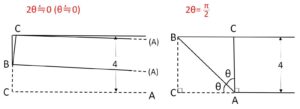
\(0<2θ<\displaystyle\frac{π}{2}\) より
\(0<θ<\displaystyle\frac{π}{4}\)
\(f(θ)=\sinθ\cos^3θ\) (\(0<θ<\displaystyle\frac{π}{4}\)) とおくと
\(f'(θ)=\cosθ\cos^3θ+\sinθ\cdot3\cos^2θ(-\sinθ)\)
\(=\cos^2θ(\cos^2θ-3\sin^2θ)\)
\(=\cos^2θ\{\cos^2θ-3(1-\cos^2θ)\}\)
\(=\cos^2θ(4\cos^2θ-3)\)
\(=\cos^2θ(2\cosθ+\sqrt{3})(2\cosθ-\sqrt{3})\)
(積の前2つは正の値、\(2\cosθ-\sqrt{3}=0\) を満たすのは\(θ=\displaystyle\frac{π}{6}\))
よって増減表は次の通り。
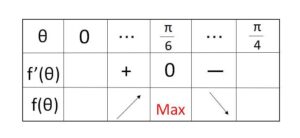
\(f(θ)\)は正の値なので、\(f(θ)\)が最大値をとるとき、三角形\(ABC\)の面積は最小となる。
よって \(θ=\displaystyle\frac{π}{6}\) のとき\(△ABC\)は最小で、
最小値は
\(\displaystyle\frac{2}{\sin\displaystyle\frac{π}{6}\cos^3\displaystyle\frac{π}{6}}=\)\(\displaystyle\frac{32\sqrt{3}}{9}\)
(例題2)
座標平面において、点\(P(0,1)\) を中心とする半径\(1\)の円を\(C\)とする。\(a\)を \(0<a<1\) を満たす実数とし、直線 \(y=a(x+1)\) と\(C\)との交点を\(Q,R\)とする。
(1)\(△PQR\)の面積\(S(a)\)を求めよ。
(2)\(a\)が \(0<a<1\) の範囲を動くとき、\(S(a)\)が最大となる\(a\)を求めよ。
(解答)
(1)
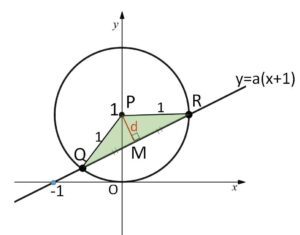
\(P\)から直線\(QR\)に降ろした垂線の足を\(M\)とすると、\(M\)は線分\(QR\)の中点となる。
直線\(QR\)の方程式は
\(ax-y+a=0\)
だから
\(d=PM=\displaystyle\frac{|0-1+a|}{\sqrt{a^2+1}}=\)\(\displaystyle\frac{1-a}{\sqrt{a^2+1}}\) (∵ \(0<a<1\) )
また
\(QM=\sqrt{1^2-d^2}=\sqrt{1-\displaystyle\frac{(1-a)^2}{a^2+1}}\)
\(=\sqrt{\displaystyle\frac{2a}{a^2+1}}\)
より
\(QR=2\sqrt{\displaystyle\frac{2a}{a^2+1}}\)
したがって
\(S(a)=\displaystyle\frac{1}{2}\cdot2\sqrt{\displaystyle\frac{2a}{a^2+1}}\cdot\displaystyle\frac{1-a}{\sqrt{a^2+1}}\)
\(=\displaystyle\frac{\sqrt{2a}(1-a)}{a^2+1}\)
(2)
\(S(a)=\displaystyle\frac{\sqrt{2a}(1-a)}{a^2+1}\) (\(0<a<1\))
(\(\sqrt{a}(1-a)=a^{\frac{1}{2}}-a^{\frac{3}{2}}\) より)
\(S'(a)=\sqrt{2}\cdot\displaystyle\frac{(\displaystyle\frac{1}{2\sqrt{a}}-\displaystyle\frac{3}{2}\sqrt{a})(a^2+1)-\sqrt{a}(1-a)\cdot2a}{(a^2+1)^2}\)
(分母分子に \(2\sqrt{a}\) を掛けて)
\(=\sqrt{2}\cdot\displaystyle\frac{(1-3a)(a^2+1)-2a(1-a)\cdot2a}{2\sqrt{a}(a^2+1)^2}\)
\(=\sqrt{2}\cdot\displaystyle\frac{a^3-3a^2-3a+1}{2\sqrt{a}(a^2+1)^2}\)
(\(a=-1\) のとき分子\(0\)だから \((a+1)\) が因数)
\(=\sqrt{2}\cdot\displaystyle\frac{(a+1)(a^2-4a+1)}{2\sqrt{a}(a^2+1)^2}\)
\(a^2-4a+1=0\) の解は
\(a=2±\sqrt{3}\)
であるから、\(0<a<1\) における増減表は次の通り。
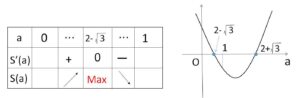
したがって、\(S(a)\)が最大となるのは
\(a=2-\sqrt{3}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→対数微分法と最大・最小値 back→最大・最小値と係数決定