方程式の解の極限の例題です。
(例題1)
\(m\)を\(2\)以上の自然数、\(e\)は自然対数の底とする。
(1)方程式 \(xe^x-me^x+m=0\) を満たす正の実数\(x\)の値はただ1つであることを示せ。またその値を\(c\)とするとき、\(m-1<c<m\) となることを示せ。
(2)\(x>0\) の範囲で \(f(x)=\displaystyle\frac{e^x-1}{x^m}\) は \(x=c\) で最小となることを示せ。
(3)\(a_m\)を(2)で求められる\(f(x)\)の最小値とするとき、\(\displaystyle\lim_{m \to \infty}\displaystyle\frac{\log a_m}{m\log m}\) を求めよ。
(解答)
(1)
このとき左辺をそのまま \(y=g(x)\) とおいたほうが、\(y=0\) 付近を考えればよいことになるので楽です。定数分離ももちろん手段の1つですが、今回はかえって面倒になります。
\(xe^x-me^x+m=0\)
\(g(x)=xe^x-me^x+m\) とおくと
\(g'(x)=(e^x+xe^x)-me^x\)
\(=e^x\{x-(m-1)\}\)
よって \(x≧0\) における増減表は次の通り。
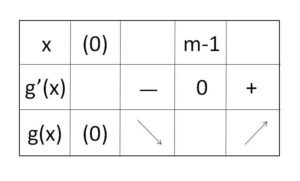
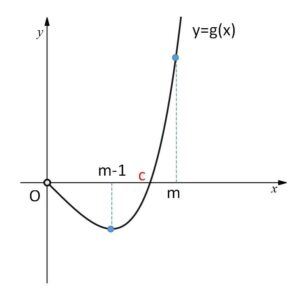
また増減表より \(g(m-1)<0\) であり
\(g(m)\)\(=me^m-me^m+m=m\)\(>0\)
したがって \(y=g(x)\) のグラフは上図のようになり、\(g(x)=0\) の正の実数解はただ1つであり、その解\(c\)は、\(m-1<c<m\) を満たす。
(2)
\(f(x)=\displaystyle\frac{e^x-1}{x^m}\)
\(f'(x)=\displaystyle\frac{e^xx^m-(e^x-1)\cdot mx^{m-1}}{x^{2m}}\)
\(=\displaystyle\frac{xe^x-me^x+m}{x^{m+1}}\)
\(=\displaystyle\frac{g(x)}{x^{m+1}}\)
\(x>0\) において \(x^{m+1}>0\) なので、\(f'(x)\) と \(g(x)\) の符号は一致する。
\(g(x)\) の符号は(1)より
\(0<x<c\) のとき \(g(x)<0\)
\(x=c\) のとき \(g(x)=0\)
\(x>c\) のとき \(g(x)>0\)
となるから、\(f(x)\) は \(x=c\) で最小値をとる。
(3)
\(ce^c-me^c+m=0\)
が成り立ちます。\(c\)は(1)で \(m-1<c<m\) と評価されているので、これを用いてはさみうちの原理を利用します。
(2)より
\(a_m=\displaystyle\frac{e^c-1}{c^m}\)・・・①
また、\(x=c\) は(1)の方程式の解なので
\(ce^c-me^c+m=0\)
よって
\(e^c-1=\displaystyle\frac{ce^c}{m}\)・・・②
②を①に代入して (分子の差の形を解消する)
\(a_m=\displaystyle\frac{ce^c}{mc^m}\)
ゆえに
\(\displaystyle\frac{\log a_m}{m\log m}\)\(=\displaystyle\frac{\log\displaystyle\frac{ce^c}{mc^m}}{m\log m}\)
\(=\displaystyle\frac{\log c+c-\log m-m\log c}{m\log m}\)
\(=\displaystyle\frac{1}{m}\cdot(\displaystyle\frac{\log c}{\log m})+(\displaystyle\frac{c}{m})\cdot\displaystyle\frac{1}{\log m}-\displaystyle\frac{1}{m}-(\displaystyle\frac{\log c}{\log m})\)
(\(c\)と\(m\)、\(\log c\)と\(\log m\) でまとめた)
ここで \(m-1<c<m\)・・・③ だから
\(1-\displaystyle\frac{1}{m}<\displaystyle\frac{c}{m}<1\)
はさみうちの原理より
\(\displaystyle\lim_{m \to \infty}\displaystyle\frac{c}{m}=1\)
また③より
\(\log (m-1)<\log c<\log m\)
となるから
\(\displaystyle\frac{\log(m-1)}{\log m}<\displaystyle\frac{\log c}{\log m}<1\)
(左辺の分子の\(\log\)の中身を\(m\)でくくって、\(1\)に収束することを示します)
(左辺)=\(\displaystyle\frac{\log m(1-\displaystyle\frac{1}{m})}{\log m}=1+\displaystyle\frac{\log(1-\displaystyle\frac{1}{m})}{\log m}\)
となるから、はさみうちの原理より
\(\displaystyle\lim_{m \to \infty}\displaystyle\frac{\log c}{\log m}=1\)
したがって
\(\displaystyle\lim_{m \to \infty}\displaystyle\frac{\log a_m}{m\log m}\)
\(=0\cdot1+1\cdot0-0-1\)
\(=-1\)
(例題2)
\(n=1,2,\cdots\) に対して\(x\)の整式
\(P_n(x)=x^3-nx^2-(2n+12)x-8\)
を考える。以下の問に答えよ。
(1)3次方程式 \(P_n(x)=0\) の正の実数解はただ1つであることを示せ。
(2)\(t\)が \(P_n(x)=0\) の解であるとき、\(P_n(-\displaystyle\frac{4}{t+2})\) を求めよ。
(3)\(P_n(x)=0\) の正の実数解を\(α_n\)とするとき、\(P_n(x)=0\) の最小の実数解\(β_n\)を\(α_n\)で表せ。さらに、\(\displaystyle\lim_{n \to \infty}β_n\) を求めよ。
(解答)
(1)
\(P_n(x)=x^3-nx^2-(2n+12)x-8\)
微分して
\(P_n'(x)=3x^2-2nx-(2n+12)\)
\(P_n'(x)=0\) を満たすのは
\(x=\displaystyle\frac{n±\sqrt{n^2+6n+36}}{3}\)
\(n\)は自然数だから\(x\)は実数。これを小さい順に \(x_1,x_2\) とおくと、\(x_1<0\)、\(x_2>0\)
よって \(x≧0\) における増減表は次の通り。
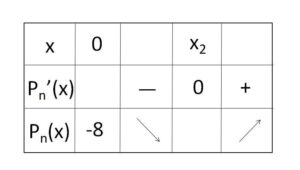
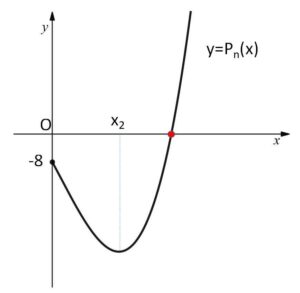
\(P_n(0)=-8\)、\(\displaystyle\lim_{x \to \infty}P_n(x)=\infty\) に注意すると、グラフは上図のようになるので、 \(P_n(x)=0\) の正の実数解はただ1つである。
(2)
\(P_n(x)=x^3-nx^2-(2n+12)x-8\)
\(P_n(x)=0\) の解が\(t\)だから
\(t^3-nt^2-(2n+12)t-8=0\)・・・①
\(P_n(-\displaystyle\frac{4}{t+2})\)
\(=(-\displaystyle\frac{4}{t+2})^3-n(-\displaystyle\frac{4}{t+2})^2-(2n+12)(-\displaystyle\frac{4}{t+2})-8\)
\(=\displaystyle\frac{-64-16n(t+2)+4(2n+12)(t+2)^2-8(t+2)^3}{(t+2)^3}\)
\(=\displaystyle\frac{8}{(t+2)^3}\cdot\{-t^3+nt^2+(2n+12)t+8\}\)
\(=0\) (①より)
(3)
残り1つの解(の候補)は、解と係数の関係を用いて求めてよいですが、次のようにして求めると後々\(t\)による場合分けを省くことができます。
「\(x=t\) が解 → \(x=-\displaystyle\frac{4}{t+2}\) も解」より
「\(-\displaystyle\frac{4}{t+2} \ (=u)\) が解 → \(x=-\displaystyle\frac{4}{-\displaystyle\frac{4}{t+2} +2} \ (=-\displaystyle\frac{4}{u+2})\) も解」
(さらにこの操作をもう1回行うと \(x=t\) に戻ります)
(2)より
\(P_n(x)=0\) について
\(x=t\) が解だと、\(x=-\displaystyle\frac{4}{t+2}\)・・・② も解となるので
②の\(t\)を \(-\displaystyle\frac{4}{t+2}\) におきかえた
\(x=-\displaystyle\frac{4}{-\displaystyle\frac{4}{t+2}+2}=\displaystyle\frac{-2(t+2)}{-2+(t+2)}=\)\(\displaystyle\frac{-2(t+2)}{t}\)・・・③
も解になる。
\(x=t,-\displaystyle\frac{4}{t+2},\displaystyle\frac{-2(t+2)}{t}\)
となり、正の実数解を\(α_n\)が、\(t\)の値によってどれになるか変わってきます。
しかし、先ほどの要領でもう1つの解を作ろうとすると\(t\)に戻ることから、結局どれを正の解\(α_n\)としても、3つの解(の候補)が同じ式で表されます。よって \(t>0\) として、\(t=α_n\) としても問題なしです。
また③の\(t\)を \(-\displaystyle\frac{4}{t+2}\) におきかえると
\(x=-2-4\cdot(-\displaystyle\frac{t+2}{4})=t\)
に戻るので、\(x=t,-\displaystyle\frac{4}{t+2},\displaystyle\frac{-2(t+2)}{t}\) のどれを正の解 \(α_n\) としても、3式は
\(α_n,-\displaystyle\frac{4}{α_n+2},\displaystyle\frac{-2(α_n+2)}{α_n}\)
で表される。
\(α_n>0\) より
\(-\displaystyle\frac{4}{α_n+2}<0,\ \displaystyle\frac{-2(α_n+2)}{α_n}<0\)
だから、これらは \(α_n\) とは異なる負の実数解である。
また大小比較をすると
\(-\displaystyle\frac{4}{α_n+2}-(\displaystyle\frac{-2(α_n+2)}{α_n})\)
\(=\displaystyle\frac{-4α_n+2(α_n+2)^2}{α_n(α_n+2)}\)
\(=\displaystyle\frac{2α_n^2+4α_n+8}{α_n(α_n+2)}\)\(>0\)
より、\(-\displaystyle\frac{4}{α_n+2}>\displaystyle\frac{-2(α_n+2)}{α_n}\)
よって、\(P_n(x)=0\) の3つの異なる実数解は
\(α_n,-\displaystyle\frac{4}{α_n+2},\displaystyle\frac{-2(α_n+2)}{α_n}\)
であり、左から大きい順になっている。ゆえに最小の実数解\(β_n\)は
\(β_n=-2-\displaystyle\frac{4}{α_n}\)
(1)のグラフより、極値をとる\(x_2\)より\(α_n\)が大きいことと、\(x_2 \to \infty\) から、\(α_n \to \infty\) です。
また(1)のグラフより
\(x_2<α_n\)
だから
\(\displaystyle\frac{n+\sqrt{n^2+6n+36}}{3}<α_n\)
\(n \to \infty\) のとき (左辺)\(\to \infty\) だから
\(\displaystyle\lim_{n \to \infty}α_n=\infty\)
したがって
\(\displaystyle\lim_{n \to \infty}β_n\)\(=\displaystyle\lim_{n \to \infty}(-2-\displaystyle\frac{4}{α_n})\)
\(=-2\)
\(P_n(x)=0\) の「解の1つは正の実数解であることは確定」・・・(i) しています。
また、「\(x=t\) を解とすると、\(-\displaystyle\frac{4}{t+2},\displaystyle\frac{-2(t+2)}{t}\) も解」・・・(ii) です。
(ii)は\(t\)の値に関係なく成り立つことなので、(i)も合わせると \(t>0\) として、残り2つを負の実数解として大小比較して、3つの実数解を揃えるという方針でもよいと思います。(上の解答はやりすぎかもしれません)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→数値の大小 back→n次方程式の解と微分