高次方程式と微分に関する例題です。
(例題1)
\(a_1,a_2,\cdots,a_n\) を、\(a_1<a_2<\cdots<a_n\) を満たす実数とする。\(n\)を\(2\)以上の整数とし、
\(f(x)=(x-a_1)(x-a_2)\cdots\cdots(x-a_n)\)
とする。このとき次の方程式はそれぞれ、\(a_k\) と \(a_{k+1}\) (\(k=1,2,\cdots,n-1\)) の間に実数解をもつことを示せ。
(1)\(f'(x)=0\)
(2)\(\displaystyle\frac{1}{x-a_1}+\displaystyle\frac{1}{x-a_2}+\cdots+\displaystyle\frac{1}{x-a_n}=0\)
(解答)
(1)
\(f(x)=(x-a_1)(x-a_2)\cdots\cdots(x-a_n)\)
\(f'(x)=(x-a_2)(x-a_3)\cdots(x-a_n)\) (1つ目を微分)
\(+(x-a_1)(x-a_3)\cdots(x-a_n)\) (2つ目を微分)
\(+\cdots\cdots\)
\(+(x-a_1)(x-a_2)\cdots(x-a_{n-2})(x-a_n)\) (n-1つ目を微分)
\(+(x-a_1)(x-a_2)\cdots(x-a_{n-2})(x-a_{n-1})\) (nつ目を微分)
ここで
\(f'(a_n)=0+0+\cdots+(a_n-a_1)(a_n-a_2)\cdots(a_n-a_{n-2})(a_n-a_{n-1})\)
だから、\(a_1<a_2<\cdots<a_n\) より
\(f'(a_n)>0\)
(\(x=a_1\) から始めると、\(n\)の偶奇や\(f'(a_1)\)の正負の場合分けが必要になる)
同様に
\(f'(a_{n-1})=(a_{n-1}-a_1)(a_{n-1}-a_2)\cdots(a_{n-1}-a_{n-2})\color{blue}{(a_{n-1}-a_n)}\)
だから、\(f'(a_{n-1})<0\) (最後の項だけ負になる)
これを繰り返すことで
\(f'(a_{n-2})>0\)、\(f'(a_{n-3})<0\)・・・となり、隣合う \(f'(a_{k+1})\) と \(f'(a_{k})\) の符号が異なることになる。
よって\(f'(x)\)は連続なので、方程式 \(f'(x)=0\) は\(a_k\)と\(a_{k+1}\)の間に実数解をもつ。
\(f'(x)=0\) は1回微分しているので、\(n-1\)次方程式。これよりすべての解が出揃っていることになります。
(注)
2つの積の微分は
\((f_1f_2)’=f_1’f_2+f_1f_2’\)
で、これを利用すると3つの積の微分は
\((f_1f_2f_3)’=\{f_1(f_2f_3)\}’=f_1′(f_2f_3)+f_1(f_2f_3)’\)
\(=f_1’f_2f_3+f_1f_2’f_3+f_1f_2f_3’\)
となります。
さらに、3つの積の微分を利用すると4つの積については
\((f_1f_2f_3f_4)’=\{f_1(f_2f_3f_4)\}’\)
\(=f_1′(f_2f_3f_4)+f_1(f_2f_3f_4)’\)
\(=f_1’f_2f_3f_4+f_1f_2’f_3f_4+f_1f_2f_3’f_4+f_1f_2f_3f_4’\)
となります。
これを繰り返すことで(正確には帰納法を使う)
\((f_1f_2\cdots\cdots f_{n-1}f_{n})’\)
\(=f_1’f_2\cdots f_{n-1}f_{n}+f_1f_2’\cdots f_{n-1}f_{n}+\)
\(\cdots+f_1f_2\cdots f_{n-1}’f_{n}+f_1f_2\cdots f_{n-1}f_{n}’\)
となり、積のどれか1つを微分したものの和になっています。
(参考1)
直接\(f'(a_k),f'(a_{k+1})\)の符号を考えてもよいです。
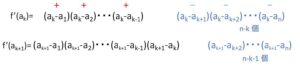
\(f'(a_k)=(a_k-a_1)(a_k-a_2)\cdots(a_k-a_{k-1})\color{blue}{(a_k-a_{k+1})(a_k-a_{k+2})\cdots(a_k-a_n)}\)
は\(0\)ではないので、正か負。
いずれにせよ、\(f'(a_{k+1})\) では積のうち負の部分が1個減るので、\(f'(a_{k})\) とは符号が異なる。
(参考2)
\(f(x)=(x-a_1)(x-a_2)\cdots\cdots(x-a_n)\)
より
\(f(a_1)=0\)、\(f(a_2)=0\)、・・・、\(f(a_n)=0\)
なので、平均値の定理(ロルの定理)を用いるとスッキリ証明できます。
\(f(x)\)は(連続かつ)微分可能で、\(f(a_k)=0\)、\(f(a_{k+1})=0\) より
\(f'(c)=0\) (\(a_k<c<a_{k+1}\))
を満たす\(c\)が存在することなります。つまり \(f'(x)=0\) の解が\(c\)で、\(c\)は\(a_k\)と\(a_{k+1}\)の間の実数です。
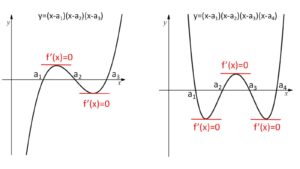
参考として \(n=3,4\) の場合の \(y=f(x)\) のグラフを載せておきます。
(2)
よって \(f'(x)=0\) の解を考えればよいのですが、これらの解を代入したときに分母が\(0\)にならないことの確認はしておきます。
\(\displaystyle\frac{1}{x-a_1}+\displaystyle\frac{1}{x-a_2}+\cdots+\displaystyle\frac{1}{x-a_n}=0\)・・・①
より
\(\displaystyle\frac{f'(x)}{f(x)}=0\)
(1)より、方程式 \(f'(x)=0\) は\(a_k\)と\(a_{k+1}\)の間に実数解をもつ。
またその解 \(x=α\) は \(a_1,a_2,\cdots,a_n\) とは異なるので、\(f(α)=0\) とはならない。
したがって、方程式①は\(a_k\)と\(a_{k+1}\)の間に実数解をもつ。
(例題2)
関数 \(f_n(x)\) を
\(f_n(x)=1+x+\displaystyle\frac{x^2}{2}+\displaystyle\frac{x^3}{3}+\cdots+\displaystyle\frac{x^n}{n}\) (\(n=1,2,3,\cdots\))
で定める。
(1)\(n\)が偶数のとき、\(x\)の方程式 \(f_n(x)=0\) は実数解をもたないことを示せ。
(2)\(n\)が\(3\)以上の奇数のとき、\(x\)の方程式 \(f_n(x)=0\) は \(-2<x<-1\) の範囲にただ1つの実数解をもつことを示せ。
\(f_n'(x)=1+x+x^2+\cdots+x^{n-1}\)
となります。さらに等比数列の和から
\(f_n'(x)=\displaystyle\frac{1-x^n}{1-x}\) (\(x≠1\))
とまとめることができます。等比数列の和に気づかない場合の別解もあります。
(解答)
(1)
\(f_n(x)=1+x+\displaystyle\frac{x^2}{2}+\displaystyle\frac{x^3}{3}+\cdots+\displaystyle\frac{x^n}{n}\)
微分して
\(f_n'(x)=1+x+x^2+\cdots+x^{n-1}\)・・・①
(以下\(f’_n(x)\)の符号を考えますが、\(x≧0\) のときは明らかに正になるので、\(x<0\)の場合だけを吟味します)
(i)\(x≧0\)のとき
①より \(f_n'(x)>0\)
(ii)\(x<0\)のとき
①より
\(f_n'(x)=\displaystyle\frac{1-x^{n}}{1-x}\)
\(n=2k\) (\(k=1,2,\cdots\)) より
\(f_n'(x)=\displaystyle\frac{1-x^{2k}}{1-x}\)
\(1-x>0\) より、\(1-x^{2k}\) の符号を考えればよく、\(x^{2k} \ (>0)\)の単調性から
\(1-x^{2k}=0\) を満たすのは \(x=-1\) のみ。
(i)(ii)より増減表は次の通り。
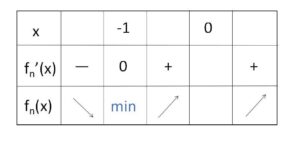
最小値は (正になることを示せばよい)
\(f_n(-1)=1-1+\displaystyle\frac{1}{2}-\displaystyle\frac{1}{3}+\cdots-\displaystyle\frac{1}{2k-1}+\displaystyle\frac{1}{2k}\)
(2項ずつまとめて)
\(=(\displaystyle\frac{1}{2}-\displaystyle\frac{1}{3})+(\displaystyle\frac{1}{4}-\displaystyle\frac{1}{5})+\cdots(\displaystyle\frac{1}{2k-2}-\displaystyle\frac{1}{2k-1})+\displaystyle\frac{1}{2k}\)\(>0\)
よって
\(f_n(x)>0\) となるから、\(f_n(x)=0\) の実数解は存在しない。
(別解)
\(f_n'(x)=1+x+x^2+\cdots+x^{n-1}\) (\(n\)は偶数)
\(f_n'(x)=0\) の実数解が \(x=-1\) であることを発見できたら、\((x+1)\)が因数になることが分かるので、割り算して因数分解するか、もしくは次のようにして因数分解できる。
\(f_n'(x)=(1+x)+x^2(1+x)+\cdots+x^{n-2}(1+x)\)
\(=(1+x)(1+x^2+x^4+\cdots+x^{n-2})\)
積の2つ目はすべて偶数乗なので、正。よって \(x+1\) の符号だけを考えればよいことになる。
これで\(f_n(x)\)の増減が分かるので、あとは解答と同じように \(f_{n}(-1)>0\) を示せばよい。
(2)
\(f_n'(x)=1+x+x^2+\cdots+x^{n-1}\)・・・①
(i)\(x≧0\)のとき
①より \(f_n'(x)>0\)
(ii)\(x<0\)のとき
①より
\(f_n'(x)=\displaystyle\frac{1-x^{n}}{1-x}\)
\(n=2k+1\) (\(k=1,2,\cdots\)) より
\(f_n'(x)=\displaystyle\frac{1-x^{2k+1}}{1-x}>0\) (分母分子ともに正)
よって\(f_n(x)\)は単調増加。
また
\(f_n(-1)=1-1+\displaystyle\frac{1}{2}-\displaystyle\frac{1}{3}+\cdots+\displaystyle\frac{1}{2k}-\displaystyle\frac{1}{2k+1}\)
\(=(\displaystyle\frac{1}{2}-\displaystyle\frac{1}{3})+\cdots+(\displaystyle\frac{1}{2k}-\displaystyle\frac{1}{2k+1})\)
よって、\(f_n(-1)>0\)
(\(n=1\) のときは、\(f_n(-1)=0\) となってしまうので、\(n≧3\) の条件になっている)
\(f_n(-2)=1-2+\displaystyle\frac{2^2}{2}-\displaystyle\frac{2^3}{3}+\cdots+\displaystyle\frac{2^{2k}}{2k}-\displaystyle\frac{2^{2k+1}}{2k+1}\)
\(=-1+(\displaystyle\frac{2^2}{2}-\displaystyle\frac{2^3}{3})+\cdots+(\displaystyle\frac{2^{2k}}{2k}-\displaystyle\frac{2^{2k+1}}{2k+1})\)
ここで
\(\displaystyle\frac{2^{2k}}{2k}-\displaystyle\frac{2^{2k+1}}{2k+1}=\displaystyle\frac{2^{2k}(1-2k)}{2k(2k+1)}<0\) (\(k=1,2,\cdots\))
だから
\(f_n(-2)<0\)
したがって
方程式 \(f_n(x)=0\) は \(-2<x<-1\) の範囲にただ1つの実数解をもつ。
(別解)
\(f_n'(x)=1+x+x^2+\cdots+x^{n-1}\) (\(n\)は奇数)
(i)\(x≧0\) のとき \(f’_n(x)>0\)
(ii)\(x<0\) のとき
\(f_n'(x)=1+x+x^2+\cdots+x^{2k}\)
(ア)\(x≦-1\) のとき
\(f_n'(x)=1+(x+x^2)+(x^3+x^4)+\cdots+(x^{2k-1}+x^{2k})\)
\(=1+x(1+x)+x^3(1+x)+\cdots+x^{2k-1}(1+x)\)\(>0\)
(\(1+x≦0\)、\(x,x^3,\cdots x^{2k-1}<0\) より)
(イ)\(-1<x<0\) のとき
\(f_n'(x)=(1+x)+(x^2+x^3)+\cdots+(x^{2k-2}+x^{2k-1})+x^{2k}\)
\(=(1+x)+x^2(1+x)+\cdots+x^{2k-2}(1+x)+x^{2k}\)\(>0\)
(\(1+x>0\)、 \(x^2,x^4,\cdots,x^{2k}>0\) より)
以上より任意の実数\(x\)で \(f_n'(x)>0\) となるから、\(f_n(x)\)は単調増加。
(以下解答と同様のため省略)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→方程式の解と極限 back→同形出現と微分