まずは2次方程式の解の個数問題からです。→(6-2)2次方程式の実数解の個数 と内容は条件式が2次不等式になること以外は同じです。
(問題1)
次の方程式の解の個数を求めよ。ただし\(k\)は定数とする。
\(kx^2+(3k+1)x+2(k+1)=0\)
(解答)
(1)\(k=0\)のとき 与式は
\(x+2=0\)となり 解は \(x=-2\)の1個
(2)\(k≠0\)のとき 判別式を\(D\)として
\(D=(3k+1)^2-4k・2(k+1)\)
\(=k^2-2k+1\)
\(=(k-1)^2\)
よって \(k=1\)のとき \(D=0\)より解は1個(重解)
\(k≠1\)のとき \(D>0\)より解は2個
以上(1)(2)より
\(k<0\)のとき2個
\(k=0\)のとき1個
\(0<k<1\)のとき2個
\(k=1\)のとき1個(重解)
\(k>1\)のとき2個
続いて、2次不等式の解の存在に関する問題です。
(問題2)
\(x\)の2次不等式 \(x^2-2ax+2a^2+2a-1<0\) が解をもつような\(a\)の範囲を求めよ。
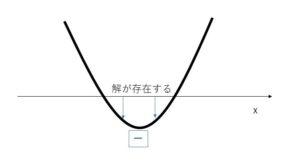
左辺の2次関数のグラフは下に凸なので、解をもつためには\(x\)軸と2点で交わり、負の部分がありさえすればいいので条件は\(D>0\)のみです。
(解答)
題意を満たす条件は、与式の(左辺)\(=0\)の判別式\(D\)について\(D>0\)
\(\displaystyle\frac{D}{4}\)\(=a^2-(2a^2+2a-1)\)
\(=-a^2-2a+1>0\)
よって \(a^2+2a-1<0\)・・・①
題意を満たす条件は、与式の(左辺)\(=0\)の判別式\(D\)について\(D>0\)
\(\displaystyle\frac{D}{4}\)\(=a^2-(2a^2+2a-1)\)
\(=-a^2-2a+1>0\)
よって \(a^2+2a-1<0\)・・・①
\(a^2+2a-1=0\) を解くと \(x=-1±\sqrt{2}\) なので
①の解は \(-1-\sqrt{2}<a<-1+\sqrt{2}\)
これが求める\(a\)の範囲である。
①の解は \(-1-\sqrt{2}<a<-1+\sqrt{2}\)
これが求める\(a\)の範囲である。
(問題3)
2次不等式 \(kx^2+(k+3)x+k>0\)が解をもたないような、定数\(k\)の値の範囲を求めよ。
2次不等式 \(kx^2+(k+3)x+k>0\)が解をもたないような、定数\(k\)の値の範囲を求めよ。
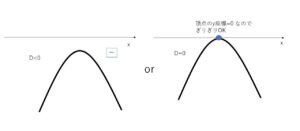
今度は解をもたない条件です。まず下に凸の場合は必ずグラフに正の部分が存在するため題意を満たすには、上に凸すなわち\(k<0\)。あとは正の部分が存在しなければいいので、\(x\)軸とグラフが2点で交わらない、すなわち判別式が0以下の値です。
(解答)
題意を満たすには、すべての\(x\)で \(kx^2+(k+3)x+k≦0\)
2次不等式より\(k≠0\)で 求める条件は
\(k<0\) かつ \(D≦0\)
題意を満たすには、すべての\(x\)で \(kx^2+(k+3)x+k≦0\)
2次不等式より\(k≠0\)で 求める条件は
\(k<0\) かつ \(D≦0\)
\(D=(k+3)^2-4k^2\)
\(=-3k^2+6k+9≦0\)
よって \(k^2-2k-3≧0\) \((k+1)(k-3)≧0\) から
\(=-3k^2+6k+9≦0\)
よって \(k^2-2k-3≧0\) \((k+1)(k-3)≧0\) から
\(k≦-1\) または \(k≧3\)
\(k<0\)を満たすのは
\(k≦-1\)
\(k≦-1\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。