円と曲線に囲まれうる図形の面積の例題です。
(例題1)
2つの曲線
\(x^2+y^2=1\)、\(y≧0\)・・・①
\(y=\displaystyle\frac{1}{4x}\)・・・②
の2つの交点の\(x\)座標を、それぞれ\(p,q\) (ただし \(p<q\)) とする。
(1))\(\cos\displaystyle\frac{α}{2}=p\)、\(\cos\displaystyle\frac{β}{2}=q\) をみたす\(α,β\) を求めよ。ただし、\(0<α<π\)、\(0<β<π\) とする。
(2)曲線①と②で囲まれた部分の面積を求めよ。
(解答)
(1)
直接交点を \((\cosθ,\sinθ)\) とおくと有名角の三角比にならないので\(\displaystyle\frac{θ}{2}\) という誘導がついています。
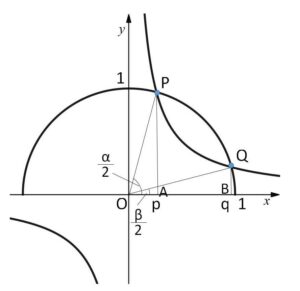
図のように点を設定する。交点は第1象限にあるので、\(x>0\)。
\(x^2+y^2=1\)、\(y≧0\)・・・①
\(y=\displaystyle\frac{1}{4x}\)・・・②
②を①に代入して
\(x^2+\displaystyle\frac{1}{16x^2}=1\)
\(16x^4-16x^2+1=0\)
(\(x^2\)の2次方程式として解くと)
\(x^2=\displaystyle\frac{8±\sqrt{48}}{16}=\displaystyle\frac{2±\sqrt{3}}{4}(>0)\)
交点の\(x\)座標を \(\cos\displaystyle\frac{θ}{2}\) とおくと、\(x=\cos\displaystyle\frac{θ}{2}\) であり
\(\cosθ=2\cos^2θ-1=\displaystyle\frac{2±\sqrt{3}}{2}-1=±\displaystyle\frac{\sqrt{3}}{2}\)
\(0<θ<π\) より
\(θ=\displaystyle\frac{π}{6},\displaystyle\frac{5}{6}π\)
ゆえに
\(\displaystyle\frac{θ}{2}=\displaystyle\frac{π}{12},\displaystyle\frac{5}{12}π\)
よって、\(p<q\) (\(\cos\displaystyle\frac{α}{2}<\cos\displaystyle\frac{β}{2}\)) に注意すると
\(\displaystyle\frac{α}{2}=\displaystyle\frac{5}{12}π\)、\(\displaystyle\frac{β}{2}=\displaystyle\frac{π}{12}\)
したがって
\(α=\displaystyle\frac{5}{6}π\)、\(β=\displaystyle\frac{1}{6}π\)
(2)
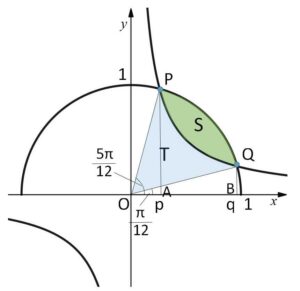
求める面積を\(S\)とすると
\(S=扇形OPQ-T\)
\(=\displaystyle\frac{1}{2}\cdot1^2\cdot\displaystyle\frac{4π}{12}-(△OAP+\displaystyle\int_{p}^{q}\displaystyle\frac{1}{4x}dx-△OBQ)\)
\(=\displaystyle\frac{π}{6}-\left(\displaystyle\frac{1}{2}p\cdot\displaystyle\frac{1}{4p}+\displaystyle\frac{1}{4}\log\displaystyle\frac{q}{p}-\displaystyle\frac{1}{2}q\cdot\displaystyle\frac{1}{4q}\right)\)
\(=\displaystyle\frac{π}{6}-\displaystyle\frac{1}{4}\log\displaystyle\frac{q}{p}\)
ここで(1)より
\(x^2=\displaystyle\frac{2±\sqrt{3}}{4}\) であり、\(0<p<q\) だから
\(p=\displaystyle\frac{\sqrt{2-\sqrt{3}}}{2}\)、\(q=\displaystyle\frac{\sqrt{2+\sqrt{3}}}{2}\)
よって
\(S=\displaystyle\frac{π}{6}-\displaystyle\frac{1}{4}\log\sqrt{\displaystyle\frac{2+\sqrt{3}}{2-\sqrt{3}}}\)
\(=\displaystyle\frac{π}{6}-\displaystyle\frac{1}{8}\log\displaystyle\frac{2+\sqrt{3}}{2-\sqrt{3}}\)
\(=\displaystyle\frac{π}{6}-\displaystyle\frac{1}{8}\log\displaystyle\frac{(2+\sqrt{3})^2}{1}\)
\(=\displaystyle\frac{π}{6}-\displaystyle\frac{1}{4}\log(2+\sqrt{3})\)
(例題2)
\(f(x)=\log\displaystyle\frac{x^2+1}{2}\) とおく。\(xy\)平面上の円\(C\)と曲線\(D:y=f(x)\)は\(D\)のすべての変曲点で接しているとする。ただし、2つの曲線がある点で接するとはその点で共通の接線をもつことをいう。
(1)円\(C\)の方程式を求めよ。
(2)\(C\)と\(D\)の共有点は\(D\)の変曲点のみであることを証明せよ。
(3)\(C\)と\(D\)で囲まれた部分の面積を求めよ。
(解答)
(1)
\(y=f(x)\) が\(y\)軸対称であることから円の中心は\(y\)座標にあることは分かるので解答の目安にはしておきます。
変曲点が接点になっているので、まずこれから求めてみます。
\(f(x)=\log\displaystyle\frac{x^2+1}{2}=\log(x^2+1)-\log2\) より
\(f'(x)=\displaystyle\frac{2x}{x^2+1}\)
\(f”(x)=\displaystyle\frac{2(x^2+1)-2x\cdot 2x}{(x^2+1)^2}=\displaystyle\frac{2(1-x^2)}{(x^2+1)^2}\)
よって変曲点の\(x\)座標は、\(x=±1\) だから
変曲点は \(A(-1,0),B(1,0)\)
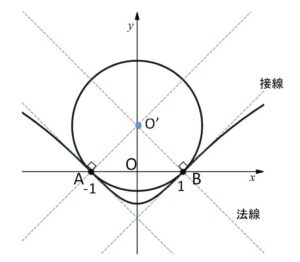
\(C,D\)がこの変曲点で接しているので、2つの変曲点における法線の交点が円の中心となる。
法線の方程式はそれぞれ
\(y=(x+1)\)、\(y=-(x-1)\)
だから、連立すると
\((x,y)=(0,1)\)
半径\(r\)は \((0,1)\) と \(A(-1,0)\) の距離を考えて
\(r=\sqrt{1^2+1^2}=\sqrt{2}\)
したがって円の方程式は
\(x^2+(y-1)^2=2\)
(2)
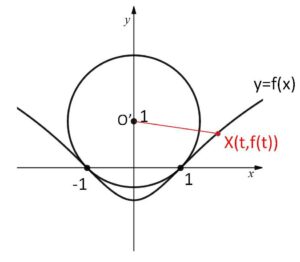
円と曲線\(y=f(x)\)は、\(y\)軸について対称だから、\(x≧0\) だけ考えればよい。
円の中心\(O'(0,1)\) と、\(y=f(x)\) 上の点 \(X(t,\log\displaystyle\frac{t^2+1}{2})\) の距離の2乗は
\(O’X^2=t^2+(\log\displaystyle\frac{t^2+1}{2}-1)^2\) (\(t≧0\))
これを\(g(t)\)とおくと
\(g'(t)=2t+2(\log\displaystyle\frac{t^2+1}{2}-1)\cdot\displaystyle\frac{2t}{t^2+1}\)
\(=\displaystyle\frac{2t}{t^2+1}\left(t^2+1+2\log\displaystyle\frac{t^2+1}{2}-2\right)\)
(複雑な式ですが、\(t=1\)のみで最小値をとることを意識して進めていきます)
ここで
\(h(t)=t^2+1+2\log\displaystyle\frac{t^2+1}{2}-2\)
は単調増加関数で、\(h(1)=0\) を満たすので
\(0≦t≦1\) のとき \(g(t)\)は単調減少
\(t≧1\) のとき \(g(t)\)は単調増加
となるから、\(t=1\) のときのみ 最小値 \(g(1)=2\) をとる。
したがって \(0≦t<1\)、\(t>1\) では
\(O’X>\sqrt{2}\) となるから、変曲点以外に共有点は存在しない。
(3)
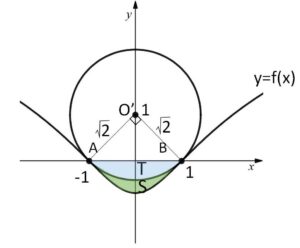
図より求める面積\(S\)は
\(S=\displaystyle\int_{-1}^{1}(-\log\displaystyle\frac{x^2+1}{2})dx-T\)
(偶関数の積分、\(T\)は扇形と三角形の差で求まる)
\(=-2\displaystyle\int_{0}^{1}\log\displaystyle\frac{x^2+1}{2}dx-\left\{\displaystyle\frac{1}{2}\cdot(\sqrt{2})^2\cdot\displaystyle\frac{π}{2}-\displaystyle\frac{1}{2}\cdot(\sqrt{2})^2\right\}\)
(\(\log\)の積分なので部分積分)
\(=-2\left[x\log\displaystyle\frac{x^2+1}{2}\right]_{0}^{1}+2\displaystyle\int_{0}^{1}x\cdot\displaystyle\frac{2x}{x^2+1}dx-\left(\displaystyle\frac{π}{2}-1\right)\)
\(=4\displaystyle\int_{0}^{1}\displaystyle\frac{x^2}{x^2+1}dx-\left(\displaystyle\frac{π}{2}-1\right)\)
(分子の次数が大きいので帯分数の形に)
\(=4\displaystyle\int_{0}^{1}\left(1+\displaystyle\frac{-1}{x^2+1}\right)dx-\left(\displaystyle\frac{π}{2}-1\right)\)
(\(x=\tanθ\) の置換をして)
\(=4[x]_{0}^{1}-4[θ]_{0}^{\frac{π}{4}}-\left(\displaystyle\frac{π}{2}-1\right)\)
\(=4-π-\left(\displaystyle\frac{π}{2}-1\right)\)
\(=5-\displaystyle\frac{3}{2}π\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→極限と面積(減衰曲線) back→媒介変数と面積③(内外サイクロイド)