極座標で表された曲線が囲む面積の例題です。
\(x=r\cosθ=f(θ)\cosθ\)
\(y=r\sinθ=f(θ)\sinθ\)
により媒介変数表示にするのが基本です。
(例題)
\(xy\)平面上で原点を極、\(x\)軸の正の部分を始線とする極座標に関して、極方程式 \(r=2+\cosθ\) (\(0≦θ≦π\)) により表される曲線を\(C\)とする。\(C\)と\(x\)軸とで囲まれた図形の面積を求めよ。
(解答)
\(r=2+\cosθ\) (\(0≦θ≦π\)) より曲線\(C\)は次のように媒介変数表示できる。
\(x=(2+\cosθ)\cosθ\)
\(y=(2+\cosθ)\sinθ\)
\(\displaystyle\frac{dx}{dθ}=-2\sinθ+2\cosθ(-\sinθ)\)
\(=-2\sinθ(1+\cosθ)\)
よって \(0<θ<π\) では、\(x\) は単調減少。
また、\(y=(2+\cosθ)\sinθ≧0\) であり
\(y=0\) を満たすのは、\(θ=0,π\)。このとき \(x=3,-1\)
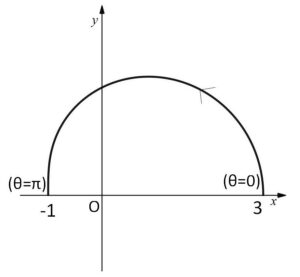
したがって面積\(S\)は
\(S=\displaystyle\int_{-1}^{3}ydx\)
(置換積分をする。\(dx=-2\sinθ(1+\cosθ)dθ\)。積分区間の対応には注意)
\(=\displaystyle\int_{π}^{0}(2+\cosθ)\sinθ\cdot(-2)\sinθ(1+\cosθ)dθ\)
\(=2\displaystyle\int_{0}^{π}(2+\cosθ)(1+\cosθ)\sin^2θdθ\)
(\(\cosθ\) に統一する)
\(=2\displaystyle\int_{0}^{π}(2+\cosθ)(1+\cosθ)(1-\cos^2θ)dθ\)
\(=2\displaystyle\int_{0}^{π}(2+3\cosθ-\cos^2θ-3\cos^3θ-\cos^4θ)dθ\)
(\(\cos^2θ,\cos^4θ\)は2倍角の公式を利用する。\(\cos^3θ\)は3倍角の公式か導関数接触型にする)
ここで
\(\displaystyle\int_{0}^{π}dθ=π\)
\(\displaystyle\int_{0}^{π}\cosθdθ=[\sinθ]_{0}^{π}=0\)
\(\displaystyle\int_{0}^{π}\cos^2θdθ=\displaystyle\int_{0}^{π}\displaystyle\frac{1+\cos2θ}{2}dθ=\displaystyle\frac{1}{2}π\)
\(\displaystyle\int_{0}^{π}\cos^3θdθ=\displaystyle\int_{0}^{π}(1-\sin^2θ)\cosθdθ\)
\(=\left[\sinθ-\displaystyle\frac{\sin^3θ}{3}\right]_{0}^{π}=0\)
\(\displaystyle\int_{0}^{π}\cos^4θdθ=\displaystyle\int_{0}^{π}(\displaystyle\frac{1+\cos2θ}{2})^2dθ\)
\(=\displaystyle\int_{0}^{π}(\displaystyle\frac{1}{4}+\displaystyle\frac{\cos2θ}{2}+\displaystyle\frac{\cos^22θ}{4})dθ\)
\(=\displaystyle\int_{0}^{π}(\displaystyle\frac{1}{4}+\displaystyle\frac{\cos2θ}{2}+\displaystyle\frac{1+\cos4θ}{8})dθ\)
\(=\displaystyle\frac{π}{4}+\displaystyle\frac{π}{8}=\displaystyle\frac{3}{8}π\)
となるから
\(S=2\left(2π-\displaystyle\frac{1}{2}π-\displaystyle\frac{3}{8}π\right)\)
\(=\displaystyle\frac{9}{4}π\)
(参考)極方程式による面積公式
極方程式 \(r=f(θ)\) (\(α≦θ≦β\)) で表される曲線上の点と極\(O\)を結んだ線分が通過する領域の面積は
\(S=\displaystyle\int_{α}^{β}\displaystyle\frac{1}{2}r^2dθ\)
で表されることを利用しても解くことができます。(入試等で使うのはおすすめしない)
\(S=\displaystyle\int_{0}^{π}\displaystyle\frac{1}{2}(2+\cosθ)^2dθ\)
\(=\displaystyle\frac{1}{2}\displaystyle\int_{0}^{π}(4+2\cosθ+\cos^2θ)dθ\)
\(=\displaystyle\frac{1}{2}\displaystyle\int_{0}^{π}(4+2\cosθ+\displaystyle\frac{1+\cos2θ}{2})dθ\)
\(=\displaystyle\frac{1}{2}\left[\displaystyle\frac{9}{2}θ+2\sinθ+\displaystyle\frac{\sin2θ}{4}\right]_{0}^{π}\)
\(=\displaystyle\frac{9}{4}π\)
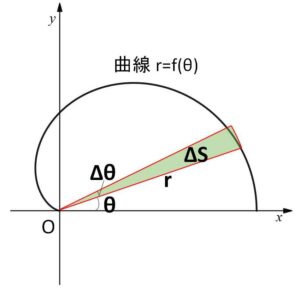
証明は簡易的には、微小な扇形の面積を考えると
\(ΔS≒\displaystyle\frac{1}{2}r^2Δθ\)
よって
\(\displaystyle\frac{ΔS}{Δθ}≒\displaystyle\frac{1}{2}r^2\) より
\(S=\displaystyle\int_{α}^{β}\displaystyle\frac{1}{2}r^2dθ\)
丁寧に証明すると
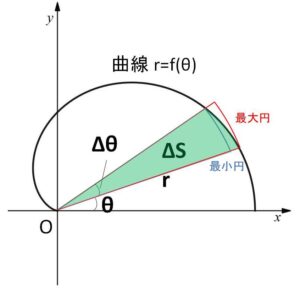
\(θ\)から\(θ+Δθ\) までの、\(r=f(θ)\) の最大値と最小値をそれぞれ\(r_M,r_m\)とすると、微小面積\(ΔS\)について次の不等式が成り立つ。(最大円と最小円の扇形の間にある)
\(\displaystyle\frac{1}{2}r_m^2Δθ≦ΔS≦\displaystyle\frac{1}{2}r_M^2Δθ\)
\(Δθ>0\) のとき (\(Δθ<0\)のときも不等号が逆向きになるだけで結論は同じ)
\(\displaystyle\frac{1}{2}r_m^2≦\displaystyle\frac{ΔS}{Δθ}≦\displaystyle\frac{1}{2}r_M^2\)
\(Δθ \to 0\) のとき、\(r_m,r_M \to r\) となるから
\(\displaystyle\frac{dS}{dθ}=\displaystyle\frac{1}{2}r^2\)
あとは積分すればよい。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→断面積と体積 back→逆関数と面積