媒介変数表示された曲線で囲まれる図形の回転体の体積を求める例題です。
(i)媒介変数を消去する。(可能なら)
(ii)媒介変数のまま置換積分を利用して解く。
の2パターン解法になります。(ii)の方法は媒介変数が消去できるかどうかに関わらず使えるので重要解法です。\(x,y\)をそれぞれ媒介変数で微分してグラフの概形をかくことが基本ですが、特に気を付けるのが\(x\)で積分する際に\(y\)が\(x\)の関数になっているかどうかの確認です。これは\(x\)の単調増加(減少)性で簡単に確認できますが、単調でない場合には分割して考えることになります。(例題2参照)
(例題1)
座標平面において、サイクロイド
\(x=θ-\sinθ\)、\(y=1-\cosθ\) (\(0≦θ≦2π\))
と\(x\)軸で囲まれた図形を、\(x\)軸まわりに回転してできる立体の体積を求めよ。
\(\displaystyle\frac{dx}{dθ}\) から\(x\)の単調性が分かり、\(y≧0\) より\(x\)軸にまたがっていないのでそのまま積分してよいことになります。
これらのことはグラフを書けば分かりますが、意識しているだけで随分違います。
(解答)
\(x=θ-\sinθ\)、\(y=1-\cosθ\) (\(0≦θ≦2π\))
\(\displaystyle\frac{dx}{dθ}=1-\cosθ≧0\) (単調増加)
\(\displaystyle\frac{dy}{dθ}=\sinθ\) (\(θ=π\) で極大)
と、\(θ=0,2π\) のとき \(x=0,2π\)、\(y=0\) だからサイクロイドのグラフは次のようになる。
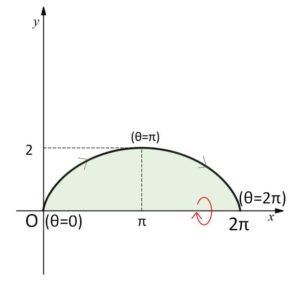
よって求める体積\(V\)は、\(dx=(1-\cosθ)dθ\) より
\(V=π\displaystyle\int_{0}^{2π}y^2dx\)
(置換積分する。積分区間の対応に注意)
\(=π\displaystyle\int_{0}^{2π}(1-\cosθ)^2(1-\cosθ)dθ\)
\(=π\displaystyle\int_{0}^{2π}(1-3\cosθ+3\cos^2θ-\cos^3θ)dθ\)
(2乗は倍角の公式、3乗は3倍角の公式 or 導関数接触型にする)
\(=π\displaystyle\int_{0}^{2π}\left\{1-3\cosθ+\displaystyle\frac{3(1+\cos2θ)}{2}-\cosθ(1-\sin^2θ)\right\}dθ\)
\(=π\displaystyle\int_{0}^{2π}\left(\displaystyle\frac{5}{2}-4\cosθ+\displaystyle\frac{3}{2}\cos2θ+\sin^2θ\cosθ\right)dθ\)
\(=π\left[\displaystyle\frac{5}{2}θ-4\sinθ+\displaystyle\frac{3}{4}\sin2θ+\displaystyle\frac{1}{3}\sin^3θ\right]_{0}^{2π}\)
\(=5π^2\)
(例題2)
\(xy\)平面上の曲線\(C\)
\(\begin{eqnarray} \left\{ \begin{array}{l} x=(1+\cosθ)\cosθ \\ y =(1+\cosθ)\sinθ \end{array} \right. \end{eqnarray}\) (\(0≦θ≦π\))
と\(x\)軸で囲まれた領域を\(D\)とする。\(D\)を\(x\)軸のまわりに1回転してできる回転体の体積を求めよ。
(解答)
\(\begin{eqnarray} \left\{ \begin{array}{l} x=(1+\cosθ)\cosθ \\ y =(1+\cosθ)\sinθ \end{array} \right. \end{eqnarray}\) (\(0≦θ≦π\))
\(\displaystyle\frac{dx}{dθ}=-\sinθ\cosθ+(1+\cosθ)(-\sinθ)\)
\(=-\sinθ(2\cosθ+1)\)
\(\displaystyle\frac{dy}{dθ}=-\sinθ\sinθ+(1+\cosθ)\cosθ\)
\(=\cos^2θ-1+\cosθ+\cos^2θ\)
\(=(\cosθ+1)(2\cosθ-1)\)
よって \(-(2\cosθ+1)\)、\(2\cosθ-1\) の符号を考えればよく、増減表とグラフは次のようになる。
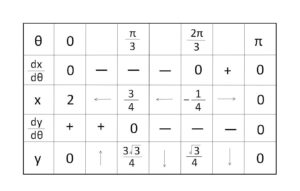
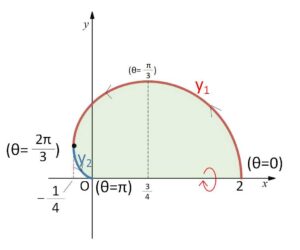
したがって体積\(V\)は
\(V=π\displaystyle\int_{-\frac{1}{4}}^{2}y_1^2dx-π\displaystyle\int_{-\frac{1}{4}}^{0}y_2^2dx\)
(\(dx=-\sinθ(2\cosθ+1)dθ\)。積分区間の対応に注意)
\(=π\displaystyle\int_{\frac{2}{3}π}^{0}y^2(θ)(-\sinθ)(2\cosθ+1)dθ-π\displaystyle\int_{\frac{2}{3}π}^{π}y^2(θ)(-\sinθ)(2\cosθ+1)dθ\)
(区間をつなげて)
\(=π\displaystyle\int_{0}^{π}y^2(θ)\sinθ(2\cosθ+1)dθ\)
\(=π\displaystyle\int_{0}^{π}(1+\cosθ)^2\sin^2θ\sinθ(2\cosθ+1)dθ\)
(導関数接触型。\(\sinθ\)を1つの残して残りを\(\cosθ\)にする)
\(=π\displaystyle\int_{0}^{π}(1+\cosθ)^2(1-\cos^2θ)(2\cosθ+1)\sinθdθ\)
(\(\cosθ= t\) で置換)
\(=π\displaystyle\int_{1}^{-1}(1+t)^2(1-t^2)(2t+1)(-1)dt\)
\(=π\displaystyle\int_{-1}^{1}(1+t)^2(1-t^2)(2t+1)dt\)
\(=π\displaystyle\int_{-1}^{1}(-t^4-2t^3+2t+1)(2t+1)dt\)
(偶奇関数の定積分。奇数乗はすべて\(0\)になる)
\(=2π\displaystyle\int_{0}^{1}(-5t^4+4t^2+1)dt\)
\(=2π\left[-t^5+\displaystyle\frac{4}{3}t^3+t\right]_{0}^{1}\)
\(=\displaystyle\frac{8}{3}π\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→極座標と回転体 back→重複部分と回転体