回転させる図形が、\(x\)軸について上下 (\(y\)軸について左右) に存在する場合の例題です。
この場合一方を折り返して、片側に寄せるのが基本です。
(例題)
\(a\)を \(0≦a<\displaystyle\frac{π}{2}\) の範囲にある実数とする。2つの直線 \(x=0\)、\(x=\displaystyle\frac{π}{2}\) および 2つの曲線 \(y=\cos(x-a)\)、\(y=-\cos x\) によって囲まれる図形を\(G\)とする。
(1)図形\(G\)を\(x\)軸の周りに1回転させてできる立体の体積を\(V\)とする。\(V\)を\(a\)を用いて表せ。
(2)\(a\)を条件の範囲で変化させる。\(V\)の最大値とそのときの\(a\)の値を求めよ。
(解答)
(1)
よって一方を折り返すことになります。(解答では下半分を折り返すことにします)
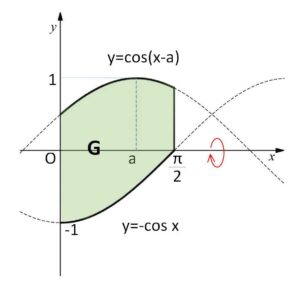
\(0≦x≦\displaystyle\frac{π}{2}\) のとき \(0≦a<\displaystyle\frac{π}{2}\) より
\(-\displaystyle\frac{π}{2}<x-a≦\displaystyle\frac{π}{2}\)
よって、\(\cos(x-a)≧0\) となるから、図形\(G\)を図示すると上記のようになる。
図形\(G\)の \(y≦0\) の部分を\(x\)軸について折り返してできる図形の回転体の体積が求める\(V\)である。
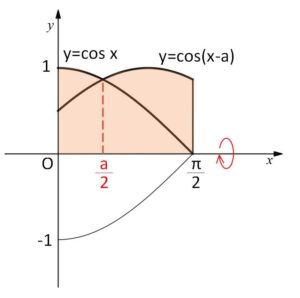
\(\cos x=\cos(x-a)\) を解くと
\(\cos x-\cos(x-a)=0\)
\(-2\sin\displaystyle\frac{2x-a}{2}\sin\displaystyle\frac{a}{2}=0\)
よって、\(0≦x≦\displaystyle\frac{π}{2}\) における \(y=\cos x\) と \(y=\cos(x-a)\) の交点の\(x\)座標は、
\(a≠0\) のとき
\(-\displaystyle\frac{a}{2}≦x-\displaystyle\frac{a}{2}≦\displaystyle\frac{π}{2}-\displaystyle\frac{a}{2}\) と \(0<a<\displaystyle\frac{π}{2}\) より
\(x-\displaystyle\frac{a}{2}=0\) つまり \(x=\displaystyle\frac{a}{2}\)
また \(a=0\) のときは \(y=\cos x\) の回転体を考えればよいので、\(V\)は\(a=0\)の場合も含めて次のように表される。
\(V=π\displaystyle\int_{0}^{\frac{a}{2}}\cos^2xdx+π\displaystyle\int_{\frac{a}{2}}^{\frac{π}{2}}\cos^2(x-a)dx\)
\(=π\displaystyle\int_{0}^{\frac{a}{2}}\displaystyle\frac{1+\cos2x}{2}dx+π\displaystyle\int_{\frac{a}{2}}^{\frac{π}{2}}\displaystyle\frac{1+\cos(2x-2a)}{2}dx\)
\(=\displaystyle\frac{π}{2}\left[x+\displaystyle\frac{1}{2}\sin2x\right]_{0}^{\frac{a}{2}}+\displaystyle\frac{π}{2}\left[x+\displaystyle\frac{1}{2}\sin(2x-2a)\right]_{\frac{a}{2}}^{\frac{π}{2}}\)
\(=\displaystyle\frac{π}{2}(\displaystyle\frac{a}{2}+\displaystyle\frac{1}{2}\sin a)+\displaystyle\frac{π}{2}\{\displaystyle\frac{π}{2}+\displaystyle\frac{1}{2}\sin(π-2a)-\displaystyle\frac{a}{2}-\displaystyle\frac{1}{2}\sin(-a)\}\)
\(=\displaystyle\frac{π}{2}(\displaystyle\frac{a}{2}+\displaystyle\frac{1}{2}\sin a)+\displaystyle\frac{π}{2}(\displaystyle\frac{π}{2}+\displaystyle\frac{1}{2}\sin2a-\displaystyle\frac{a}{2}+\displaystyle\frac{1}{2}\sin a)\)
\(=\displaystyle\frac{π}{4}(\sin 2a+2\sin a+π)\)
(2)
(微分するだけです)
\(f(a)=\sin 2a+2\sin a+π\) (\(0≦a<\displaystyle\frac{π}{2}\)) とおく。
\(f'(a)=2\cos2a+2\cos a\)
\(=2(2\cos^2a-1)+2\cos a\)
\(=2(2\cos^2a+\cos a-1)\)
\(=2(2\cos a-1)(\cos a+1)\)
よって \(a=\displaystyle\frac{π}{3}\) のとき \(f(a)\)は最大値をとるので
このとき\(V\)も最大値
\(V_{MAX}=\displaystyle\frac{π}{4}f(\displaystyle\frac{π}{3})\)
\(=\displaystyle\frac{π}{4}(\displaystyle\frac{\sqrt{3}}{2}+\displaystyle\frac{2\sqrt{3}}{2}+π)\)
\(=\displaystyle\frac{π}{8}(3\sqrt{3}+2π)\)
をとる。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→媒介変数表示と回転体 back→陰関数と回転体