連立不等式の表す立体の体積を求める例題です。
(例題)
\(xyz\)空間において、不等式
\(0≦z≦1+x+y-3(x-y)y\)
\(0≦y≦1\)
\(y≦x≦y+1\)
のすべてを満足する\((x,y,z)\)を座標にもつ点全体がつくる立体の体積を求めよ。
断面の取り方は \(x,y,z\)軸に垂直な断面の3パターンが考えられますが、どれを選択するかはなるべく断面が簡単になるようするのが目安です。
この例題だと、1つ目の不等式で\(x,y\)が2次式、2つの目の式で\(y\)は定数範囲で表されていることなどを考慮して\(y\)軸に垂直な断面で考えるのがよいです。慣れない内は \(y=k\) のように文字定数で固定するとよいです。\(y\)が固定されると、\(xz\)平面での領域を考えて\(k(y)\)で積分という流れになります。
(解答)
\(y=k\) のときの立体の断面\(S(k)\)を考える。不等式より
\(0≦z≦1+x+k-3(x-k)k\)・・・①
\(0≦k≦1\)・・・②
\(k≦x≦k+1\)・・・③
①は
\(0≦z≦(1-3k)x+3k^2+k+1\) (\(z\)を\(x\)の関数とみるため変形した)
となる。この右辺に\(x=k,k+1\)を代入すると
\(x=k\) のとき \(\color{blue}{2k+1}>0\)
\(x=k+1\) のとき
\((1-3k)(k+1)+3k^2+k+1=\color{blue}{-k+2}>0\)
よって①③を\(xz\)平面に図示すると、傾きが正の場合だと下図のようになる。
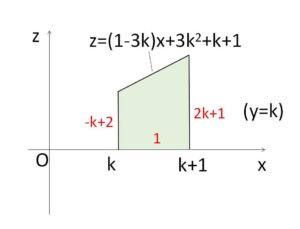
台形の面積を考えると
\(S(k)=\displaystyle\frac{1}{2}(-k+2+2k+1)\cdot1\)
\(=\displaystyle\frac{1}{2}(k+3)\)
(これは傾きの正負0によらず成り立つ)
よって②より\(0\)から\(1\)まで積分すると、体積\(V\)は
\(V=\displaystyle\int_{0}^{1}\displaystyle\frac{1}{2}(k+3)dk\)
\(=\displaystyle\frac{1}{2}\left[\displaystyle\frac{1}{2}k^2+3k\right]_{0}^{1}\)
\(=\displaystyle\frac{7}{4}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→空間の回転①(線分の回転) back→斜軸の回転体