複素数の極形式による表示について見ていきます。
・複素数の極形式
三角関数を利用することで、複素数 \(z=a+bi\) をより視覚的な形で表すことが可能になります。
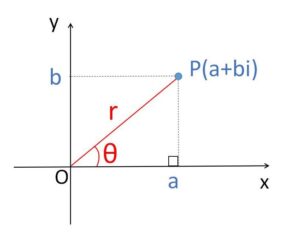
複素数平面上で\(0\)でない複素数\(z\)の表す点を\(P\)として、\(OP=r\ (=|z|=\sqrt{a^2+b^2})\)、動径\(OP\)が\(x\)軸の正の部分となす角を\(θ\)とすると
\(a=r\cosθ\)、\(b=r\sinθ\)
となるので、\(z\)を次のように表示することができます。
\(z=r(\cosθ+i\sinθ)\) (\(r>0\))・・・①
このようなの表し方①を複素数\(z\)の極形式とよびます。極形式表示により、大きさの情報\(r\)と角の情報\(θ\)が視覚的に分かることになり、さらにこれらを分離したことで後に扱う複素数の積・商の複素数平面での挙動を調べることが可能になります。
実際に \(z=a+bi\) を極形式にするには、\(r=|z|=\sqrt{a^2+b^2}\) よりこの式でくくって
\(z=\sqrt{a^2+b^2}\left(\displaystyle\frac{a}{\sqrt{a^2+b^2}}+i\displaystyle\frac{b}{\sqrt{a^2+b^2}}\right)\)
として、\(θ\)を決定することになります。
\(θ\)は偏角とよばれ
\(θ=\arg z\) (argument:偏角 の略)
で表しますが、\(\displaystyle\frac{7π}{4}\) と \(-\displaystyle\frac{π}{4}\) の動径が同じ方向であるように、偏角\(θ\)のとりかたは無数に存在します。そこで、\(0≦θ<2π\) の範囲で考えることが多いですが、\(2nπ\) (\(n\)は整数) だけズレていても位置としては同じであることから、\(2nπ\) のズレの角なら同一視するという考え方も重要です。(例えば積の偏角の公式 \(\arg(z_1z_2)=\arg z_1+\arg z_2\) は\(θ\)の範囲を限定してしまうと成り立たないケースもでてくる)
なお、\(z=0\) の場合は \(r=0\) として、\(θ\) は定義しません。
また注意点として極形式は
\(z=r(\cosθ+i\sinθ)\) (\(r>0\))・・・①
の形であり \(r>0\) はもちろん、三角関数の部分は和(\(+\))でとり、中身の角も\(θ\)で一致させる必要があります。したがって\(\bar{z}\)を極形式にすると
\(\bar{z}=r(\cosθ-i\sinθ)\)
\(=r(\cos(-θ)+i\sin(-θ))\)
です。
(例題)
次の複素数を極形式で表せ。ただし偏角\(θ\)は、\(0≦θ<2π\) とする。
(1)\(z=-1-i\)
(2)\(z=3\)
(3)\(z=-i\)
(解答)
(1)
\(z=\sqrt{1^2+1^2}(-\displaystyle\frac{1}{\sqrt{2}}+i\cdot(-\displaystyle\frac{1}{\sqrt{2}}))\)
(\(\cosθ=-\displaystyle\frac{1}{\sqrt{2}},\ \sinθ=-\displaystyle\frac{1}{\sqrt{2}}\) より \(θ=\displaystyle\frac{5π}{4}\) だから)
\(z=\sqrt{2}(\cos\displaystyle\frac{5π}{4}+i\sin\displaystyle\frac{5π}{4})\)
(2)
(\(r=3\)、\(θ=0\))
\(z=3\)
\(=3(1+i\cdot0)\)
\(=3(\cos0+i\sin0)\)
(3)
(\(r=1\)、\(θ=\displaystyle\frac{3π}{2}\))
\(z=-i\)
\(=1\cdot(0+i\cdot(-1))\)
\(=\cos\displaystyle\frac{3π}{2}+i\sin\displaystyle\frac{3π}{2}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→複素数の積・商と回転 back→実数係数のn次方程式