\(n\)次方程式とその解である複素数に関する例です。
例題に入る前に、実数係数\(n\)次方程式の重要な定理をおさらいしておきます。
・実数係数の\(n\)次方程式と虚数解
実数係数の\(n\)次方程式
\(a_nx^n+a_{n-1}x^{n-1}+\cdots+a_1x+a_0=0\)
が虚数解\(α\)をもつならば、共役複素数 \(\bar{α}\) も解である。
(解説)
係数がすべて実数であるところがポイントです(虚数係数だとこの定理は成立しない)。このとき、2つの虚数解 \(α\)と\(\bar{α}\) はセットとなります。証明は方程式の両辺について共役複素数をとるだけで簡単に示せます。
(証明)
\(α\)が解なので
\(a_nα^n+a_{n-1}α^{n-1}+\cdots+a_1α+a_0=0\)
両辺共役複素数をとって
\(\overline{a_nα^n+a_{n-1}α^{n-1}+\cdots+a_1α+a_0}=\bar{0}\)
係数は実数だから
\(a_n(\bar{α})^n+a_{n-1}(\bar{α})^{n-1}+\cdots+a_1\bar{α}+a_0=0\)
よって、\(\bar{α}\)も解である。
次に、\(n\)の偶奇で検討をしてみます。2重解,3重解・・・も2つ,3つ・・・の解としてカウント、つまり\(k\)重解を\(k\)個の解としてカウントすることにすると
\(n\)が奇数のとき、\(n-1\) 個 (偶数個) 全てが虚数解であるとすると、その和は共役複素数の和になるので実数。よって残り1つの解がもし虚数解とすると、解と係数の関係から係数\(a_{n-1}\)が虚数になってしまうので、残りの1つは実数解になります。したがって奇数次数の方程式では少なくとも1つは実数解をもちます。このことは方程式の左辺を\(f(x)\)とおいたとき、\(y=f(x)\) の概形を考えても分かります。最高次数が奇数なので、\(\displaystyle\lim_{x \to -\infty}f(x)=-\infty\)、\(\displaystyle\lim_{x \to \infty}f(x)=\infty\)。よって中間値の定理より \(f(x)=0\) となる実数\(x\)が少なくとも1つ存在することになります(少なくとも1回は\(x\)軸と交わる)。
よく扱うのが3次方程式で、1つが虚数解だと残り2つは、虚数解(共役複素数)と実数解です。
これに対して\(n\)が偶数のときは、全てが虚数解になる場合があります。
(例題1)
実数係数の3次方程式
\(x^3+x^2-x+a=0\)
が絶対値\(1\)の虚数解をもつとき、\(a\)の値と3つの解を求めよ。
残り1つは実数解ですが、これは知らなくても解けます。(解と係数の関係からすぐに分かる)
(解答)
\(x^3+x^2-x+a=0\)・・・①
の虚数解を\(α\)とおくと、\(\bar{α}\)も解。また残り1つの解を\(β\)とおく。
定数項について解と係数の関係から
\(α\bar{α}β=-a\)
\(α\)の絶対値は\(1\)だから \(|α|^2=1\) より
\(β=-a\)・・・② (\(β\)は実数であることが分かる)
\(β\)は①の解であることと②より
\(β^3+β^2-β-β=0\)
\(β(β^2+β-2)=0\)
\(β(β+2)(β-1)=0\)
よって \(β=0,-2,1\)
(あとは吟味します)
(i)\(β=0\) のとき
②より \(a=0\) だから方程式①は
\(x^3+x^2-x=0\)
\(x(x^2+x-1)=0\)
よって実数解を3つもつので不適。
(ii)\(β=-2\) のとき
②より \(a=2\) だから方程式①は
\(x^3+x^2-x+2=0\)
(\(x=-2\) が解であることを意識して)
\((x+2)(x^2-x+1)=0\)
3解は \(x=-2,\displaystyle\frac{1±\sqrt{3}i}{2}\)
これは条件を満たす。
(iii)\(β=1\) のとき
②より \(a=-1\) だから方程式①は
\(x^3+x^2-x-1=0\)
(\(x=1\) が解であることを意識して)
\((x-1)(x^2+2x+1)=0\)
\((x-1)(x+1)^2=0\)
よって実数解を3つもつので不適。
以上から
\(a=2\)、3解は \(x=-2,\displaystyle\frac{1±\sqrt{3}i}{2}\)
(例題2)
実数を係数とする3次方程式
\(x^3+px^2+qx+r=0\)
は、相異なる虚数解\(α,β\)と実数解\(γ\)をもつとする。
(1)\(β=\bar{α}\) が成り立つことを証明せよ。
(2)\(α,β,γ\) が等式
\(αβ+βγ+γα=3\)
を満たし、さらに複素数平面上で\(α,β,γ\)を表す3点は1辺の長さが\(\sqrt{3}\)の正三角形をなすものとする。このとき、実数の組 \((p,q,r)\) をすべて求めよ。
(解答)
(1)
\(x^3+px^2+qx+r=0\)
の解の1つが虚数\(α\)なので
\(α^3+pα^2+qα+r=0\)
両辺共役複素数をとって
\(\overline{α^3+pα^2+qα+r}=\bar{0}\)
\(p,q,r\)は実数だから
\((\bar{α})^3+p(\bar{α})^2+q(\bar{α})+r=0\)
よって、\(\bar{α}\)も解である。
また、\(α\)は虚数なので \(α≠\bar{α}\)
したがって、\(\bar{α}\)は\(α\)以外の虚数解となるので
\(β=\bar{α}\)
(注)
仮に \(α=\bar{α}\) (このとき実数になる) の場合には、\(α,\bar{α}\)は全く同じ解になるので \(β=\bar{α}\) と結論づけることはできません。
(2)
2解\(α,β\)は共役複素数同士になるので、複素数平面上では実軸対称の位置に存在します。正三角形の1辺の長さが\(\sqrt{3}\)であることから、\(α,β\)の虚部は \(±\displaystyle\frac{\sqrt{3}}{2}\)。
またもう1つの解の表す点\(γ\)は\(α,β\)を結ぶ線分の垂直2等分線上(実軸上)にあり(\(γ\)が実数であることと合致)、\(α,β\)を結ぶ線分から距離\(\displaystyle\frac{3}{2}\)の位置にあります。(左右の2パターンあることに注意)
よって、\(α,β\)の実部を文字\(k\)でおけば\(α,β,γ\)を\(k\)で表すことができ、後は条件式から\(k\)を決定し、最後に\(p,q,r\)を求める流れになります。
なお、\(q\)については\(3\)であることはすぐに分かります。
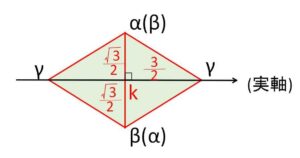
\(β=\bar{α}\) だから、\(α,β\)は実軸について対称の位置にある。
正三角形の1辺の長さは\(\sqrt{3}\)だから、\(α,β\)の実部を\(k\) (\(k\)は実数) とおくと
\(α,β\)は \(k±\displaystyle\frac{\sqrt{3}}{2}i\) と表せる。
また、正三角形の高さは\(\displaystyle\frac{3}{2}\)だから
\(γ=k+\displaystyle\frac{3}{2}\) または \(γ=k-\displaystyle\frac{3}{2}\)
と表せる。
\(αβ+βγ+γα=3\) より
\(αβ+γ(α+β)=3\)
\(k^2+\displaystyle\frac{3}{4}+2kγ=3\)・・・①
(ア)\(γ=k+\displaystyle\frac{3}{2}\) のとき
①より
\(k^2+\displaystyle\frac{3}{4}+2k(k+\displaystyle\frac{3}{2})=3\)
\(4k^2+4k-3=0\)
\((2k-1)(2k+3)=0\)
\(k=\displaystyle\frac{1}{2},-\displaystyle\frac{3}{2}\)
よって解と係数の関係から
\(p=-(α+β+γ)=-(3k+\displaystyle\frac{3}{2})\)
\(q=αβ+βγ+γα=3\)
\(r=-αβγ=-(k^2+\displaystyle\frac{3}{4})(k+\displaystyle\frac{3}{2})\)
となるから
\((p,q,r)=(-3,3,-2),\ (3,3,0)\)
(イ)\(γ=k-\displaystyle\frac{3}{2}\) のとき
①より
\(k^2+\displaystyle\frac{3}{4}+2k(k-\displaystyle\frac{3}{2})=3\)
\(4k^2-4k-3=0\)
\((2k-3)(2k+1)=0\)
\(k=\displaystyle\frac{3}{2},-\displaystyle\frac{1}{2}\)
よって解と係数の関係から
\(p=-(α+β+γ)=-(3k-\displaystyle\frac{3}{2})\)
\(q=αβ+βγ+γα=3\)
\(r=-αβγ=-(k^2+\displaystyle\frac{3}{4})(k-\displaystyle\frac{3}{2})\)
となるから
\((p,q,r)=(-3,3,0),\ (3,3,2)\)
答 \((p,q,r)=(-3,3,-2),\ (3,3,0),\ (-3,3,0),\ (3,3,2)\)
式変形だけでなく、時にはこの例題のように図形的処理も重要です。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→複素数の極形式 back→複素数の絶対値