複素数平面における三角形の形状を求める例題です。
\(\displaystyle\frac{γ-α}{β-α}=r(\cosθ+i\sinθ)\)
を求めれば、なす角\(θ\)と辺の長さの比 \(\displaystyle\frac{|γ-α|}{|β-α|}=r\) が分かり、三角形の形状が求まります。(2辺夾角相等)
(例題1)
(1)複素数\(α,β\)は、\(α^2-2αβ+4β^2=0\) を満たし、かつ \(β≠0\) とする。このとき複素数平面上で点\(α,β\)および原点\(O\)を頂点とする三角形の3辺の長さの比を求めよ。
(2)複素数\(α,β\)が関係式
\(α^2+αβ+β^2-3α-3β+3=0\)
を満たしている。ただし、\(α≠1\) とする。\(\displaystyle\frac{β-1}{α-1}\) の値を求め、複素数平面上において3点\(A(α),B(β),C(1)\)を頂点とする\(△ABC\)の形状を調べよ。
(解答)
(1)
\(α^2-2αβ+4β^2=0\)・・・①
\(β≠0\)より①の両辺を\(β^2\)で割ると
\((\displaystyle\frac{α}{β})^2-2(\displaystyle\frac{α}{β})+4=0\) (2次方程式)
\(t^2-2t+4=0\) を解くと
\(t=1±\sqrt{3}i=2\left\{\cos(±\displaystyle\frac{π}{3})+i\sin(±\displaystyle\frac{π}{3})\right\}\) だから
\(\displaystyle\frac{α}{β}=2\left\{\cos(±\displaystyle\frac{π}{3})+i\sin(±\displaystyle\frac{π}{3})\right\}\)
よって \(\angle β0α=±\displaystyle\frac{π}{3}\)、\(\displaystyle\frac{|α|}{|β|}=2\) となるから、三角形は1つの内角が\(\displaystyle\frac{π}{3}\)の直角三角形になる。
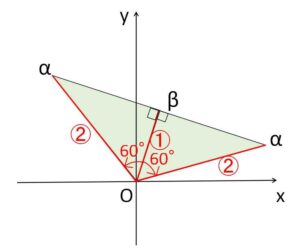
したがって3辺の長さの比は \(1:2:\sqrt{3}\)
(注)
辺の長さの比は決まりますが、この条件だけだと大きさは決まりません。また位置も、1頂点が原点であることは決まっていますが、\(α,β\)の位置は形状を保つ限りは回転させたものも条件を満たします。よって相似拡大と原点まわりの回転の分だけ無数に三角形は存在します。
(2)
\(α^2+αβ+β^2-3α-3β+3=0\)・・・②
\(α-1=A\)、\(β-1=B\) とおくと
\(α=A+1\)、\(β=B+1\)
これらを②に代入して
\((A+1)^2+(A+1)(B+1)+(B+1)^2-3(A+1)-3(B+1)+3=0\)
整理すると
\(A^2+AB+B^2=0\)・・・③
\(α≠1\) より \(A≠0\) だから、③の両辺を\(A^2\)で割って
\(1+(\displaystyle\frac{B}{A})+(\displaystyle\frac{B}{A})^2=0\)
\(t^2+t+1=0\) の解は
\(t=\displaystyle\frac{-1±\sqrt{3}i}{2}\)
よって
\(\displaystyle\frac{β-1}{α-1}\)\(=\displaystyle\frac{B}{A}\)
\(=\displaystyle\frac{-1±\sqrt{3}i}{2}\)
したがって
\(\displaystyle\frac{β-1}{α-1}=\cos(±\displaystyle\frac{2π}{3})+i\sin(±\displaystyle\frac{2π}{3})\)
となるから
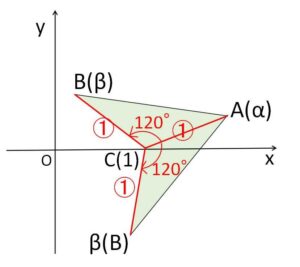
\(\angle α1β=±\displaystyle\frac{2π}{3}\)、\(\displaystyle\frac{|β-1|}{|α-1|}=1\)
より、\(△ABC\)は \(CA=CB\)、\(\angle C=\displaystyle\frac{2π}{3}\) の2等辺三角形。
(例題2)
複素数平面上に異なる3点 \(A(α),B(β),C(γ)\) がある。\(α,β,γ\)が次の関係式を満たすとき、\(△ABC\)の形状をそれぞれ調べよ。
(1)\(α+β+γ=α^2+β^2+γ^2=0\)
(2)\(α^2+β^2+γ^2-αβ-βγ-γα=0\)
(解答)
(1)
\(α+β+γ=0\)
\(α^2+β^2+γ^2=0\)
となるので、文字消去することが可能です。また第1式から、重心が原点であることはすぐに分かります。
\(α+β+γ=0\)・・・①
\(α^2+β^2+γ^2=0\)・・・②
①より
\(γ=-(α+β)\)・・・③
③を②に代入して
\(α^2+β^2+(-α-β)^2=0\)
整理して
\(α^2+αβ+β^2=0\)・・・④
(\(α\)で割りたいので \(α=0\) かどうか検討します)
ここで、\(α=0\) とすると④より \(β^2=0\)
すると \(α=β=0\) となるので異なる点であることに矛盾。
よって \(α≠0\) だから④の両辺を\(α^2\)で割って
\(1+(\displaystyle\frac{β}{α})+(\displaystyle\frac{β}{α})^2=0\)
\(t^2+t+1=0\) を解くことにより
\(\displaystyle\frac{β}{α}=\displaystyle\frac{-1±\sqrt{3}i}{2}\)
よって
\(β=\displaystyle\frac{-1±\sqrt{3}i}{2}α\)・・・⑤
これと③より
\(γ=-(α+\displaystyle\frac{-1±\sqrt{3}i}{2}α)\)
\(γ=\displaystyle\frac{-1∓\sqrt{3}i}{2}α\)・・・⑥
ゆえに\(β,γ\)の組み合わせは⑤⑥の極形式を考えると
\(β=(\cos\displaystyle\frac{2π}{3}+i\sin\displaystyle\frac{2π}{3})α\)
\(γ=(\cos\displaystyle\frac{4π}{3}+i\sin\displaystyle\frac{4π}{3})α\)
または
\(β=\left(\cos(-\displaystyle\frac{2π}{3})+i\sin(-\displaystyle\frac{2π}{3})\right)α\)
\(γ=\left(\cos(-\displaystyle\frac{4π}{3})+i\sin(-\displaystyle\frac{4π}{3})\right)α\)
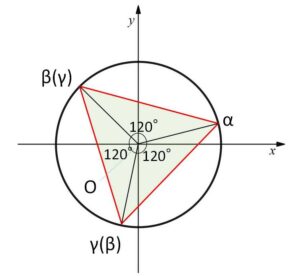
したがって大きさはそのままで、原点まわりに\(α\)を\(\displaystyle\frac{2π}{3},\displaystyle\frac{4π}{3}\)回転させたものが\(β,γ\)になるので、\(△ABC\)は外心(重心でもある)を原点とする正三角形。
(注)
\(OA=OB=OC\) と 挟角が\(120°\)であることから、\(△OAB,△OBC,△OCA\) は合同。よって\(AB=BC=CA\) となり正三角形と分かる。\(OA=OB=OC\)だから外心は原点\(O\)。正三角形なので\(O\)は重心でもある。
中心角が全て\(120°\)だからそれに対する弦の長さが等しいことから、正三角形と判断してもよい。
(2)
\(α^2+β^2+γ^2-αβ-βγ-γα=0\)・・・(i)
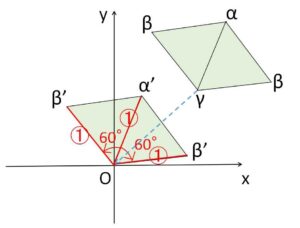
\(C(γ)\)が原点にくるように\(A(α),B(β)\)も \(-γ\) だけ平行移動させる。移動後の点を\(A'(α’),B'(β’)\)とすると、平行移動しても形状が変わらないことから\(△OA’B’\)の形状を調べればよい。
\(α’=α-γ\)、\(β’=β-γ\) だから
\(α=α’+γ\)、\(β=β’+γ\)・・・(ii)
(ii)を(i)に代入して
\((α’+γ)^2+(β’+γ)^2+γ^2-(α’+γ)(β’+γ)-(β’+γ)γ-γ(α’+γ)=0\)
整理すると
\(α’^2-α’β’+β’^2=0\)・・・(iii)
\(α≠γ\) より、\(α’≠0\) だから(iii)の両辺を\(α’^2\)で割って
\(1-(\displaystyle\frac{β’}{α’})+(\displaystyle\frac{β’}{α’})^2=0\)
よって
\(\displaystyle\frac{β’}{α’}=\displaystyle\frac{1±\sqrt{3}i}{2}=\cos(±\displaystyle\frac{π}{3})+i\sin(±\displaystyle\frac{π}{3})\)
したがって\(△OA’B’\)は正三角形になるから、\(△ABC\)も正三角形。
(別解)
\(α^2+β^2+γ^2-αβ-βγ-γα=0\)
両辺\(2\)倍して
\(2(α^2+β^2+γ^2)-2αβ-2βγ-2γα=0\)
\((α-β)^2+(β-γ)^2+(γ-α)^2=0\)・・・(a)
(以下\(α\)基準の商の形を目指す)
(a)の両辺を \((β-α)^2\) で割って
\(1+(\displaystyle\frac{β-γ}{β-α})^2+(\displaystyle\frac{γ-α}{β-α})^2=0\)
(2項目の分子を\(α\)基準にするためにいじると)
\(1+\displaystyle\frac{\{(β-α)-(γ-α)\}^2}{(β-α)^2}+(\displaystyle\frac{γ-α}{β-α})^2=0\)
\(1+1-2\cdot\displaystyle\frac{γ-α}{β-α}+(\displaystyle\frac{γ-α}{β-α})^2+(\displaystyle\frac{γ-α}{β-α})^2=0\)
よって
\((\displaystyle\frac{γ-α}{β-α})^2-\displaystyle\frac{γ-α}{β-α}+1=0\)
この2次方程式を解くと
\(\displaystyle\frac{γ-α}{β-α}=\displaystyle\frac{1±\sqrt{3}i}{2}=\cos(±\displaystyle\frac{π}{3})+i\sin(±\displaystyle\frac{π}{3})\)
したがって\(△ABC\)は正三角形となる。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→図形問題の証明と複素数 back→平行(共線)・垂直条件