平行(共線)・垂直条件

なす角を利用した平行・垂直条件について見ていきます。

・平行・垂直条件(異なる3点)
異なる3点 \(A(α),B(β),C(γ)\) について、\(AB\)と\(AC\)が平行になるための必要十分条件は、複素数の商を利用すると次のようになります。(3点だと\(A,B,C\)が同一直線上にあることになるので共線条件とも呼ばれます)

(平行条件)
\(\displaystyle\frac{γ-α}{β-α}\) が実数
つまり
\(\displaystyle\frac{γ-α}{β-α}=\overline{\left(\displaystyle\frac{γ-α}{β-α}\right)}\)

(解説)
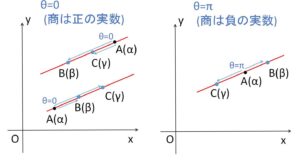
\(AB\)と\(AC\)が平行になるとき、偏角\(θ\)を \(-π<θ≦π\) に限定すると、なす角\(\angle βαγ\)が\(0\)または\(π\)となるので、商 \(\displaystyle\frac{γ-α}{β-α}\) の偏角は \(θ=0またはπ\)。

よって
\(\displaystyle\frac{γ-α}{β-α}\)
\(=R(\cos0+i\sin0)\ or \ R(\cosπ+i\sinπ)\)
\(=±R\)　(実数)

逆に、商 \(\displaystyle\frac{γ-α}{β-α}\) が実数のとき \(θ=0またはπ\) となるので\(AB\)と\(AC\)が平行になる。よって必要十分条件であることが分かる。

また偏角は向きのある角なので、\(\displaystyle\frac{γ-α}{β-α}\)が正の値になるか負の値になるかで、\(A,B,C\)の並び方が変わってきます。正の値のときは \(\angle βαγ=0\) なので、線分\(BC\)の延長線上(外部)に\(A\)があり、負の値のときは \(\angle βαγ=π\) なので、線分\(BC\)上(内部)に\(A\)が位置することになります。

同様に、\(AB\)と\(AC\)が垂直になるための必要十分条件は次のようになります。

(垂直条件)
\(\displaystyle\frac{γ-α}{β-α}\) が純虚数
つまり
\(\displaystyle\frac{γ-α}{β-α}=-\overline{\left(\displaystyle\frac{γ-α}{β-α}\right)}\)

(異なる3点なので、商が\(0\)になることはない)

(解説)
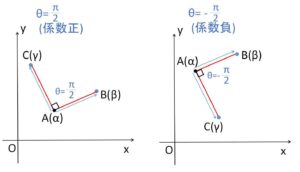
\(AB\)と\(AC\)が垂直になるとき、偏角\(θ\)を \(-π<θ≦π\) に限定すると、なす角\(\angle βαγ\)が\(±\displaystyle\frac{π}{2}\)となるので、商 \(\displaystyle\frac{γ-α}{β-α}\) の偏角は \(±\displaystyle\frac{π}{2}\)。

よって
\(\displaystyle\frac{γ-α}{β-α}\)
\(=R\{\cos(±\displaystyle\frac{π}{2})+i\sin(±\displaystyle\frac{π}{2})\}\)
\(=±Ri\)　(純虚数)

逆に、商 \(\displaystyle\frac{γ-α}{β-α}\) が純虚数のとき \(θ=±\displaystyle\frac{π}{2}\) となるので\(AB\)と\(AC\)が垂直になる。よって必要十分条件であることが分かる。

またこれも \(θ=±\displaystyle\frac{π}{2}\) のどちらをとるか(純虚数の係数が正か負か)で、位置関係が変わります。

・平行・垂直条件(異なる4点)
異なる4点 \(A(α),B(β),C(γ),D(δ)\) についても同様の平行・垂直条件が成り立ちます。

(平行条件)
\(AB /\!/ CD\)　\(⇔\)　\(\displaystyle\frac{δ-γ}{β-α}\) が実数

(垂直条件)
\(AB \perp CD\)　\(⇔\)　\(\displaystyle\frac{δ-γ}{β-α}\) が純虚数

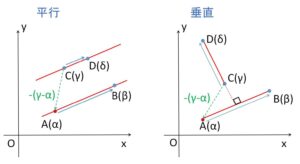
(解説)
3点の場合に帰着させればよい。例えば平行条件だと\(C\)が\(A\)に重なるように\(CD\)を \(-(γ-α)\) だけ平行移動させると、\(A(α),B(β),D'(δ-γ+α)\) の3点の平行条件を考えればよいので

\(\displaystyle\frac{(δ-γ+α)-α}{β-α}=\displaystyle\frac{δ-γ}{β-α}\)

が実数であることが平行であるための必要十分条件になる。

ベクトルに対応させると、\(β-α\) が \(\overrightarrow{AB}\)、\(δ-γ\) が \(\overrightarrow{CD}\) を表す複素数で、複素数の差(和)もベクトルと同様に位置を気にしない向きと大きさを表すものであることから、始点をすべて原点\(O\)にしても問題なく、\(β-α\) と \(δ-γ\) の商を調べることでその位置関係が分かることになります。

よって平行垂直条件に限らず、\(\displaystyle\frac{δ-γ}{β-α}\) の偏角を調べることで(始点を一致させた場合の)\(AB,CD\)のなす角が分かります。

(例題)
3個の複素数 \(-1,\ iz,\ z^2\) が複素数平面上で同一直線上にあるための\(z\)の条件を求めよ。

(解答)
(ア)3個の複素数で等しいものがあるとき
\(-1=iz\)・・・①
\(iz=z^2\)・・・②
\(z^2=-1\)・・・③

①より \(z=i\)
②より \(z(z-i)=0\)
よって \(z=0,i\)
③より、\(z=±i\)

ゆえに \(z=0,±i\) の場合には同一直線上にある。

(イ)3個の複素数が異なるとき
\(z≠0,±i\) であり
\(\displaystyle\frac{z^2-(-1)}{iz-(-1)}=\displaystyle\frac{z^2+1}{iz+1}\)

\(=\displaystyle\frac{(z+i)(z-i)}{i(z-i)}\)

\(=-iz+1\)

より、\(-iz+1\) が実数であることが同一直線上にあるための条件になる。よって \(z\) が \(z=±i\) を除く純虚数であればよい。

以上(ア)(イ)をまとめると求める条件は
\(z\)が\(0\)または純虚数

以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
next→三角形の形状　back→なす角と複素数