複素数の商を利用した4点が同一円周上にある条件について見ていきます。
・共円条件(複素数)
同一直線上にない異なる4点\(A(α),B(β),C(γ),D(δ)\)が同一円周上にある条件は次のようになります。
\(A,B,C,D\)が同一円周上にある
\(⇔\) \(\displaystyle\frac{β-γ}{α-γ}÷\displaystyle\frac{β-δ}{α-δ}\) が実数
[1]\(A,B,C,D\) or \(A,B,D,C\) の順のとき(左右周り不問)、線分\(AB\)について同じ側に\(C,D\)があるので円周角の定理を使う。
[2]\(A,C,B,D\) の順のとき(左右周り不問)、線分\(AB\)について両側に\(C,D\)があるので内接四角形の定理を使う。
で場合分けします。\(A\)を固定すると円順列により \(3!=6\) 通りの位置関係がありますが、上記3パターン×2(左右周り) で網羅しています。
(証明)
まず\(→\)について
[1]\(A,B,C,D\) or \(A,B,D,C\) の順で円周上にあるとき
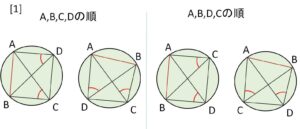
いずれも円周角の定理より
\(\angle αγβ=\angle αδβ\) となるから
\(\arg\displaystyle\frac{β-γ}{α-γ}=\arg\displaystyle\frac{β-δ}{α-δ}\)
\(\arg\displaystyle\frac{β-γ}{α-γ}-\arg\displaystyle\frac{β-δ}{α-δ}=0\)
\(\arg\left(\displaystyle\frac{β-γ}{α-γ}÷\displaystyle\frac{β-δ}{α-δ}\right)=0\)
よって
\(\displaystyle\frac{β-γ}{α-γ}÷\displaystyle\frac{β-δ}{α-δ}\) は(正の)実数となる
[2]\(A,C,B,D\) の順で円周上にあるとき
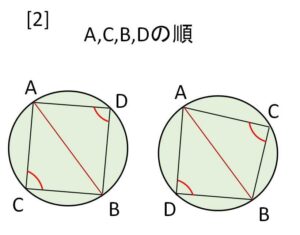
内接四角形の定理より
\(\angle αγβ+\angle βδα=±π\)
(左図の方が\(-π\))
\(\arg\displaystyle\frac{β-γ}{α-γ}+\arg\displaystyle\frac{α-δ}{β-δ}=±π\)
\(\arg\left(\displaystyle\frac{β-γ}{α-γ}×\displaystyle\frac{α-δ}{β-δ}\right)=±π\)
割り算にすると
\(\arg\left(\displaystyle\frac{β-γ}{α-γ}÷\displaystyle\frac{β-δ}{α-δ}\right)=±π\)
よって
\(\displaystyle\frac{β-γ}{α-γ}÷\displaystyle\frac{β-δ}{α-δ}\) は(負の)実数となる
\(←\)について
逆に、\(\displaystyle\frac{β-γ}{α-γ}÷\displaystyle\frac{β-δ}{α-δ}\) が実数 のとき
正の実数なら[1]、負の実数なら[2]を逆戻りすることで、
[1]\(\angle αγβ=\angle αδβ\)
[2]\(\angle αγβ+\angle βδα=±π\)
が導かれるので、それぞれ円周角の定理の逆と内接四角形の定理より4点が同一円周上にあることが示せる。
(例題)
複素数\(α\)に対してその共役複素数を\(\bar{α}\)であらわす。\(α\)を実数ではない複素数とする。複素平面内の円\(C\)が\(1,-1,α\)を通るならば、\(C\)は\(-\displaystyle\frac{1}{\bar{α}}\)も通ることを示せ。
なお複素平面とは複素数平面のことです。
また問題を解く上で必須ではありませんが \(-\displaystyle\frac{1}{\bar{α}}\) の位置については、逆数は偏角が\(-θ\)になることから、\(α \to \bar{α} \to \displaystyle\frac{1}{\bar{α}}\) で\(α\)と同じ象限に戻るので、\(-\displaystyle\frac{1}{\bar{α}}\) は\(α\)から見て原点についてちょうど反対側にあります。
(解答1)
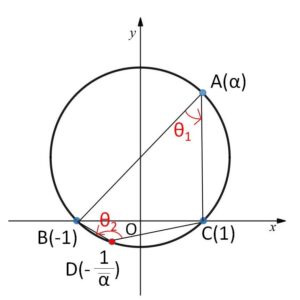
\(A\)を中心とした\(B\)から\(C\)までの回転角を\(θ_1\)、
\(D\)を中心とした\(C\)から\(B\)までの回転角を\(θ_2\)とする。
\(θ_1+θ_2\)
\(=\arg\displaystyle\frac{1-α}{-1-α}+\arg\displaystyle\frac{-1+\displaystyle\frac{1}{\bar{α}}}{1+\displaystyle\frac{1}{\bar{α}}}\)
\(=\arg\displaystyle\frac{1-α}{-1-α}+\arg\displaystyle\frac{-\bar{α}+1}{\bar{α}+1}\)
\(=\arg\left(\displaystyle\frac{1-α}{-1-α}\cdot\displaystyle\frac{-\bar{α}+1}{\bar{α}+1}\right)\)
\(=\arg\left(-\displaystyle\frac{1-α}{1+α}\cdot\displaystyle\frac{1-\bar{α}}{1+\bar{α}}\right)\)
\(=\arg\left(-\displaystyle\frac{|1-α|^2}{|1+α|^2}\right)\) (負の実数の偏角)
\(=±π\)
よって向かい合う角の和は\(180°\)となるから、4点を頂点とする四角形は円に内接する。
したがって点\(D\)は円\(C\)上にある。
(解答2)
円は\(B(-1),C(1)\)を通るので、その中心\(O’\)は虚軸上にあり、\(O'(ki)\) とおける。
半径は \(O’C=\sqrt{1^2+k^2}=\sqrt{1+k^2}\) になるから、円の方程式は
\(|z-ki|=\sqrt{1+k^2}\)
両辺2乗して
\((z-ki)(\bar{z}+ki)=1+k^2\)
つまり
\(|z|^2+(z-\bar{z})ki-1=0\)・・・①
①は点\(α\)を通るので
\(|α|^2+(α-\bar{α})ki-1=0\)・・・②
ここで①の左辺の式を\(f(z)\)とおくと
\(f(-\displaystyle\frac{1}{\bar{α}})=|-\displaystyle\frac{1}{\bar{α}}|^2+(-\displaystyle\frac{1}{\bar{α}}+\displaystyle\frac{1}{α})ki-1\)
\(=\displaystyle\frac{1}{|α|^2}+\displaystyle\frac{-α+\bar{α}}{|α|^2}ki-1\)
\(=-\displaystyle\frac{-1+(α-\bar{α})ki+|α|^2}{|α|^2}\)
\(=0\) (②より)
となるから、点\(-\displaystyle\frac{1}{\bar{α}}\)も円周上にある。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→数列の極限と複素数 back→円の方程式と極形式