2変数の確率変数の期待値・分散

2つの確率変数の期待値や分散の性質について見ていきます。
確率変数の独立がポイントになります。

・2変数の期待値の性質
(1)確率変数の和
確率変数の和の期待値は、期待値の和で計算することができます。つまり次のことが成り立ちます。

これらの等式は、確率変数が互いに独立でない場合も成り立つことに注意してください。
各変数(1変数)の期待値の和のほうが計算しやすいことが多いので、これらの等式は非常に有用です。
証明はやや難しいですが、確率変数がとる値(実現値)を\(2,3\)個に設定して(下の証明でいうと\(m,n\)を\(2～3\)に設定する)具体的に書き出すのも理解に役立つと思います。

(証明)

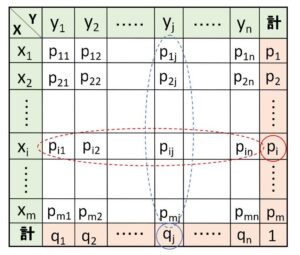
\(X\)のとる値を\(x_1,x_2,\cdots,x_m\)、\(Y\)のとる値を\(y_1,y_2,\cdots,y_n\)とする。
\(i,j\)を \(1≦i≦m\)、\(1≦j≦n\) を満たす自然数として、

\(P(X=x_i,Y=y_j)=p_{ij}\)
\(P(X=x_i)=p_i\)、\(P(Y=y_j)=q_j\)

とおく(上記表参照)。このとき

\(E(X+Y)=\displaystyle\sum_{i,j}(x_i+y_j)p_{ij}\)
(\(Z=X+Y\) とおくと、\(Z\)も確率変数であり、\(E(X+Y)\)は\(Z\)の期待値\(E(Z)\)になる)

\(=\displaystyle\sum_{i,j}x_ip_{ij}+\displaystyle\sum_{i,j}y_jp_{ij}\)　(和を分割しただけ)

(\(i,j\)のどちらから和をとり始めても、和をとる順番が変わるだけで同じになるから、1項目は\(j\)から2項目は\(i\)から和をとって)

\(=\displaystyle\sum_{i=1}^{m}x_i(p_{i1}+p_{i2}+\cdots+p_{in})+\displaystyle\sum_{j=1}^{n}y_j(p_{1j}+p_{2j}+\cdots+p_{mj})\)

(表の横方向の確率の和、縦方向の確率の和を考えて)

\(=\displaystyle\sum_{i=1}^{m}x_ip_i+\displaystyle\sum_{j=1}^{n}y_jq_j\)

\(=E(X)+E(Y)\)

また
\(E(aX+bY+c)=E(aX+(bY+c))\)

(\(bY+c\)のカタマリを1つの確率変数とみて)

\(=E(aX)+E(bY+c)\)

\(=aE(X)+bE(Y)+c\)

さらに
\(E(X_1+X_2+X_3+\cdots+X_n)\)

(\(X_2+X_3+\cdots+X_n\)のカタマリを1つの確率変数とみて)

\(=E(X_1)+E(X_2+X_3+\cdots+X_n)\)

\(=E(X_1)+E(X_2)+E(X_3+\cdots+X_n)\)

(繰り返すと)

\(=E(X_1)+E(X_2)+E(X_3)+\cdots+E(X_n)\)

以上の証明では和の取る順番などを変えているだけで、確率変数の独立の条件を一切使っていないので、独立でなくても成り立つ公式となっています。
ただし以降の内容は、独立という条件がつきます。

(2)確率変数の積
\(X,Y\)が互いに独立のとき、積の期待値について次の等式が成り立ちます。

この等式は和の分散の公式を導くのに使います。
独立であることが条件となっています。

(証明)
\(E(XY)=\displaystyle\sum_{i,j}x_iy_jp_{ij}\)

\(X,Y\)が独立だから、\(p_{ij}=p_{i}×q_{j}\) が成り立ち

\(E(XY)=\displaystyle\sum_{i,j}(x_ip_i)\cdot(y_jq_j)\)

(\(i\)のほうの和をとると、\(j\)が含まれていないのでシグマの外に出せて)

\(=(x_1p_1+x_2p_2+\cdots+x_mp_m)\displaystyle\sum_{j=1}^{n}y_jq_j\)

\(=\displaystyle\sum_{i=1}^{m}x_ip_i\displaystyle\sum_{j=1}^{n}y_jq_j\)

\(=E(X)E(Y)\)

・2変数の分散の性質
標準偏差については、分散の正の平方根をとるだけなので和の分散についてだけ検討します。
\(X,Y\)が互いに独立のとき (\(X_1,X_2,\cdots,X_n\)が互いに独立のとき) 、分散についても次の和の等式が成り立ちます。

独立という条件があるせいでややこしくなりやすいので、今回の証明では2番目の等式から始めて1個づつ丁寧にやっていきたいと思います。
1変数の場合と同じで係数\(a,b\)は2乗に拡大されて、散らばりを表す分散においては\(+c\)の分は全体が\(c\)だけ動くために影響がありません。

(証明)
\(V(X)=E(X^2)-\{E(X)\}^2\) を利用すると

\(V(aX+bY+c)\)
\(=E((aX+bY+c)^2)-\{E(aX+bY+c)\}^2\)

\(=E(a^2X^2+b^2Y^2+c^2+2abXY+2bcY+2caX)\)
\(-\{aE(X)+bE(Y)+c\}^2\)

\(=a^2E(X^2)+b^2E(Y^2)+c^2+2abE(XY)+2bcE(Y)+2caE(X)\)
\(-\{aE(X)+bE(Y)+c\}^2\)

\(=a^2[E(X^2)-\{E(X)\}^2]+b^2[E(Y^2)-\{E(Y)\}^2]\)
\(+2ab\{E(XY)-E(X)E(Y)\}\)

\(X,Y\)は独立だから、\(E(XY)-E(X)E(Y)=0\) より

\(V(aX+bY+c)=a^2V(X)+b^2V(Y)\)

\(a=b=1\)、\(c=0\) とすれば
\(V(X+Y)=V(X)+V(Y)\)

また
\(V(X_1+X_2+\cdots+X_n)\)
\(=E((X_1+X_2+\cdots+X_n)^2)-\{E(X_1+X_2+\cdots+X_n)\}^2\)
\(=E((X_1+X_2+\cdots+X_n)^2)-\{E(X_1)+E(X_2)+\cdots+E(X_n)\}^2\)

(1つ目は中身を展開して期待値の和にする。2つ目も展開して、両者をまとめると)

\(=V(X_1)+V(X_2)+\cdots+V(X_n)\)\(+2\displaystyle\sum_{k<l}\{E(X_kY_l)-E(X_k)E(Y_l)\}\)

(独立だから)

\(=V(X_1)+V(X_2)+\cdots+V(X_n)\)

(参考)共分散と無相関
実は、和の分散の等式は独立という強い条件が必須ではありません。(もちろん独立のときも成り立ちます)
簡単のため2変数
\(V(aX+bY+c)\)
について検討すると、証明の内容から

\(V(aX+bY+c)\)
\(=a^2V(X)+b^2V(Y)+2ab\{E(XY)-E(X)E(Y)\}\)

なので、
\(E(XY)=E(X)E(Y)\)・・・(i)
が成り立ちさえすれば和の等式が成り立ちます。
もちろん\(X,Y\)が互いに独立の場合(i)は成り立ちますが、独立でない場合でも(たまたま)(i)が成り立つケースがあります。(i)が成り立つとき\(X,Y\)は無相関であるといいます。
(「\(X,Y\)が独立ならば(i)が成り立つので、このとき無相関である」といえます)

数IAデータの分析のときに共分散というものを扱いましたが、確率変数についても共分散\(C(X,Y)\)は次のように定義されます。(\(m_X,m_Y\)は、それぞれ\(X,Y\)の期待値)

\(C(X,Y)=\displaystyle\sum_{i,j}(x_i-m_X)(y_i-m_Y)p_{ij}\)
\(=E((X-m_X)(Y-m_Y))\)

最後の式を変形すると
\(E((X-m_X)(Y-m_Y))\)
\(=E(XY-m_YX-m_XY+m_Xm_Y)\)
\(=E(XY)-m_YE(X)-m_XE(Y)+m_Xm_Y\)
\(=E(XY)-E(Y)E(X)-E(X)E(Y)+E(X)E(Y)\)
\(=E(XY)-E(X)E(Y)\)

となり、(i)が成り立つ、つまり無相関であることと共分散が\(0\)であることは同じ意味を表しています。よって共分散が\(0\)のときには分散の和の等式を使ってよいことになります。

共分散は平均との差の積の和であり、横軸と縦軸を\(X,Y\)とするグラフを考えれば、平均\(m_X,m_Y\)により座標平面を4分割した場合、どの領域にグラフが集中しているかを数値化したもので、\(X,Y\)の増加・減少傾向(相関)を表す量です。

次回演習を扱います。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→2変数の期待値・分散の例題　back→2変数の確率分布