和・積の期待値、和の分散に関する例題です。
2つの変数が独立かどうかには注意します。
(例題1)
表の出る確率が \(p\) (\(0<p<1\)) の硬貨を2回投げる。このとき、1回目に表が出たら \(X_1=1\)、裏が出たら \(X_1=0\)、2回目に表が出たら \(X_2=1\)、裏が出たら \(X_2=0\) であるとして、確率変数\(X_1\)と\(X_2\)とを定義する。
また、\(a,b,c\)を\(p\)に無関係な定数とする。このとき、
(1)確率変数 \(Y=aX_1+bX_2+cX_1X_2\) の期待値\(E(Y)\)を求めよ。
(2)すべての\(p\)に対して、\(E(Y)=p\) をみたし、しかも\(Y\)の分散\(V(Y)\)を最小にするように、定数\(a,b,c\)の値を定めよ。
和の期待値は独立でなくても使えますが、最後の積\(X_1X_2\)で独立が効いてきます。
(もちろん積\(X_1X_2\)自体の分布を考えても解けますが、せっかくなので前回扱った内容を駆使していきます)
(解答)
(1)
\(X_1,X_2\)は独立だから
\(E(Y)=E(aX_1+bX_2+cX_1X_2)\)
\(=aE(X_1)+b(X_2)+cE(X_1X_2)\)
\(=aE(X_1)+bE(X_2)+cE(X_1)E(X_2)\)
また\(X_1,X_2\)はいずれも次の確率分布に従う。
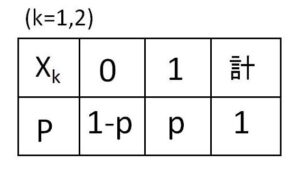
よって
\(E(X_1)=E(X_2)\)
\(=0×(1-p)+1×p\)
\(=p\)
だから
\(E(Y)=ap+bp+cp^2\)
(2)
\(E(Y)=p\) より
\(ap+bp+cp^2=p\)
\(cp^2+(a+b-1)p=0\)・・・①
①がすべての\(p\)で成り立つためには(\(p\)の恒等式だから)
\(c=0\)、\(a+b-1=0\)・・・②
よって
\(V(Y)=V(aX_1+bX_2+cX_1X_2)\)
\(=V(aX_1+bX_2)\)
(\(X_1,X_2\)は独立だから)
\(=a^2V(X_1)+b^2V(X_2)\)
(1)の表より
\(V(X_1)=V(X_2)\)
\(=E(X_1^2)-\{E(X_1)\}^2\)
\(=0^2\cdot(1-p)+1^2\cdot p-p^2\)
\(=p-p^2\)
だから
\(V(Y)=(a^2+b^2)(p-p^2)\)
\(=\{a^2+(1-a)^2\}(p-p^2)\) (②より)
\(=(2a^2-2a+1)(p-p^2)\)
\(=\left\{2(a-\displaystyle\frac{1}{2})^2+\displaystyle\frac{1}{2}\right\}(p-p^2)\)
\(0<p<1\) より \(p-p^2=p(1-p)>0\) だから
\(V(Y)\)が最小となるような\(a\)は
\(a=\displaystyle\frac{1}{2}\)
このとき②より
\(b=\displaystyle\frac{1}{2}\)
答 \(a=\displaystyle\frac{1}{2}\)、\(b=\displaystyle\frac{1}{2}\)、\(c=0\)
(例題2)
\(1\)から\(6\)までの目が\(\displaystyle\frac{1}{6}\)の確率で出るサイコロを振り、1回目に出る目を\(α\)、2回目に出る目を\(β\)とする。2次式
\((x-α)(x-β)=x^2+sx+t\)
を\(f(x)\)とおき、
\(\{f(x)\}^2=x^4+ax^3+bx^2+cx+d\)
とする。
(1)\(s\)および\(t\)の期待値を求めよ。
(2)\(a,b,c\)および\(d\)の期待値を求めよ。
(解答)
(1)
\((x-α)(x-β)=x^2+sx+t\) より
\(x^2-(α+β)+αβ=x^2+sx+t\)
よって両辺を比較すると
\(E(s)=E(-(α+β))\)・・・①
\(E(t)=E(αβ)\)・・・②
2変数\(α,β\)は題意より独立(2回のサイコロの出目は互いに影響がない)。
また、\(α,β\)はどちらも次の確率分布に従う。
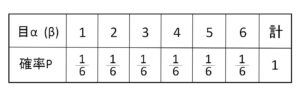
よって
\(E(α)=E(β)\)
\(=\displaystyle\frac{1}{6}(1+2+3+4+5+6)\)
\(=\displaystyle\frac{7}{2}\)
だから
①②より
\(E(s)=E(-α-β)=-E(α)-E(β)\)
\(=-7\)
\(E(t)=E(αβ)\)
\(=E(α)E(β)\) (独立より)
\(=\displaystyle\frac{49}{4}\)
(2)
積の期待値では、確実に独立であることが確認できてから利用します。
\(\{f(x)\}^2=x^4+ax^3+bx^2+cx+d\) より
\((x^2+sx+t)^2=x^4+ax^3+bx^2+cx+d\)・・・③
(1)より
\(s=-(α+β)\)、\(t=αβ\) だから
③の両辺を比較して
\(a=2s\)
\(b=s^2+2t\)
\(c=2st\)
\(d=t^2\)
だから
\(a=-2(α+β)\)・・・④
\(b=(-α-β)^2+2αβ=α^2+β^2+4αβ\)・・・⑤
\(c=-2(α+β)αβ=-2(α^2β+αβ^2)\)・・・⑥
\(d=α^2β^2\)・・・⑦
(必要なので\(α^2\)の期待値を求めておきます)
ここで
\(E(α^2)=E(β^2)\)
\(=\displaystyle\frac{1}{6}(1^2+2^2+3^2+4^2+5^2+6^2)\)
\(=\displaystyle\frac{91}{6}\)
よって④⑤⑥⑦より
\(E(a)=E(-2α-2β)\)
\(=-2E(α)-2E(β)\)
\(=-4\cdot\displaystyle\frac{7}{2}\) (\(E(α)=E(β)=\displaystyle\frac{7}{2}\))
\(=-14\)
\(E(b)=E(α^2+β^2+4αβ)\)
\(=E(α^2)+E(β^2)+4E(αβ)\)
\(=E(α^2)+E(β^2)+4E(α)E(β)\) (独立より)
\(=2\cdot\displaystyle\frac{91}{6}+4\cdot(\displaystyle\frac{7}{2})^2\)
\(=\displaystyle\frac{238}{3}\)
\(E(c)=E(-2α^2β-2αβ^2)\)
\(=-2E(α^2β)-2E(αβ^2)\)
\(E(c)=-2E((α+β)αβ)\)
と見ると、\(α+β\) と \(αβ\) は片方の\(α\)がもう一方にも存在しているので影響があるために独立ではありません。よって
\(E((α+β)αβ)=E(α+β)E(αβ)\) とやってはダメです。
(不確実な場合は安易に積の等式を利用しないほうがよいです)
\(=-2E(α^2)E(β)-2E(α)E(β^2)\) (独立より)
\(=-4\cdot\displaystyle\frac{91}{6}\cdot\displaystyle\frac{7}{2}\)
\(=-\displaystyle\frac{637}{3}\)
\(E(d)=E(α^2β^2)\)
\(=E(α^2)E(β^2)\) (\(α^2\)と\(β^2\)も確実に独立)
\(=(\displaystyle\frac{91}{6})^2\)
\(=\displaystyle\frac{8281}{36}\)
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
next→2項分布と期待値・分散 back→2変数の確率変数の期待値・分散