母集団分布

まずは標本を取り出す集団の全体(母集団)について知識を整理します。

・標本調査と母集団
ある集団を調査する場合、その全部を調査する場合と一部を調査する場合があります。
その調査の性質上必要な場合や、時間や費用が掛からない場合は集団の全部を調査することになり、それを全数調査とよびます。(例:国勢調査、テストの点数など)
これに対して、性質上不可能であったり、時間や費用が掛かったり、仮に全部を調査できたとしてもそれに見合う効果が得られない場合などは一部を調査することになり、これを標本調査とよびます。(例:ある食品会社の商品購入額、製品を傷つける必要がある工場の製品の検査など)

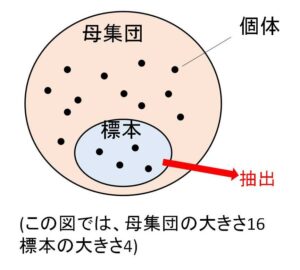
標本調査の場合、調査の対象となる全体を母集団といい、母集団に属する個々の対象を個体とよびます。また調査のために選ばれた個体の集合を標本といい、標本を選ぶことを抽出といいます。そして、個体の総数(母集団の要素の個数)を母集団の大きさ、標本に含まれる個体の個数を標本の大きさとよびます。

・抽出方法
標本の抽出は偏りがないようにする必要があります。そのため乱数表や乱数さい、コンピューターなどを利用して抽出します。このような偏りがない抽出方法を無作為抽出といい、無作為抽出された標本を無作為標本とよびます。統計的な推測では無作為抽出による抽出を採用します。

また、これとは別の観点で「復元抽出、非復元抽出」という方法があり、これについては次回で詳しく扱いたいと思いますが、少しだけ触れておきます。
復元抽出とは、文字通り1個ずつ取り出した標本を戻すことを繰り返して抽出する方法で、非復元抽出とは戻さない抽出方法です。復元抽出では母集団がその都度元通りになるので、数学的な処理が非復元抽出に比べて遥かに楽であり、できればこちらの方法を採用したいのですが、現実では1回の調査で同じ人(同じ物)を2度調査することはあまり無いので、非復元抽出をとることになってしまいます。
しかし実際の調査では、母集団の大きさが大きく、それに対して抽出する標本の大きさが小さい場合が多く、その場合は多少標本を取り出しても母集団はあまり変わらず、ほとんど復元抽出とみなせるので、特に断りが無ければ復元抽出として扱ってよいです。

・母集団分布と大きさ\(1\)の標本
例として、箱に入った次のカード全体を母集団とします。

\(1,2,3\)のカード:各\(1\)枚ずつ
\(4,5\)のカード:各\(2\)枚ずつ
\(6\)のカード:\(3\)枚
合計\(10\)枚

カードに書かれた数字に着目してこれを変量とする変数\(X\)を設定し、各値について全体に対する割合(相対度数)を考えると、その分布は次のように表すことができます。

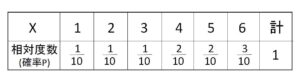
この母集団における変量の分布を母集団分布とよび、母集団分布の平均値(期待値)・分散・標準偏差をそれぞれ、母平均・母分散・母標準偏差とよびます。

ところで上記分布は、まさに母集団から\(1\)つの標本を抽出した場合の、書かれたカードの数を確率変数\(X\)とする分布になります。よってこの大きさ\(1\)の標本の変数\(X\)が従う確率分布・平均値・分散・標準偏差は、母集団分布・母平均・母分散・母標準偏差と一致することになります。

つまり、大きさ\(1\)の標本の変量を確率変数\(X\)とすると、母平均・母分散・母標準偏差がそれぞれ\(m,σ^2,σ\)であるとき

\(E(X)=m\)、\(V(X)=σ^2\)、\(σ(X)=σ\)

となります。これらのことは一般的に成り立ちます。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→復元抽出と非復元抽出(標本の選び方)　back→推測統計の概要