対称性のある立体の例題です。
対称面や対称線に着目しますが、接点や接する球の中心などはこれらの面・線上にあることが多いです。また図だけでなく、頭で空間図形をイメージして対称性をつかむのも大事です(左右対称・点対称など)。
(例題1)
一辺の長さが\(1\)の正三角形\(ABC\)を底面とする四面体\(OABC\)を考える。ただし、\(OA=OB=OC=a\) であり、\(a≧1\) とする。頂点\(O\)から三角形\(ABC\)におろした垂線の足を\(H\)とする。
(1)線分\(AH\)の長さを求めよ。
(2)\(a\)を用いて線分\(OH\)の長さを表せ。
(3)四面体\(OABC\)が球\(S\)に内接しているとする。この球\(S\)の半径\(r\)を\(a\)を用いて表せ。
(解答)
(1)
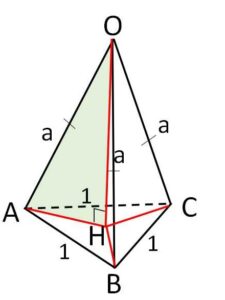
\(OH\)は共通、\(OA=OB=OC\) より、3つの直角三角形\(△OAH,△OBH,△OCH\)は合同。よって \(AH=BH=CH\) だから、\(H\)は\(△ABC\)の外心。\(△ABC\)は一辺の長さが\(1\)の正三角形だから、\(H\)は重心でもあり
\(AH=\displaystyle\frac{2}{3}\cdot\displaystyle\frac{\sqrt{3}}{2}\)\(=\displaystyle\frac{1}{\sqrt{3}}\)
(2)
三平方の定理より
\(OH=\sqrt{a^2-(\displaystyle\frac{1}{\sqrt{3}})^2}\)\(=\sqrt{a^2-\displaystyle\frac{1}{3}}\)
(3)
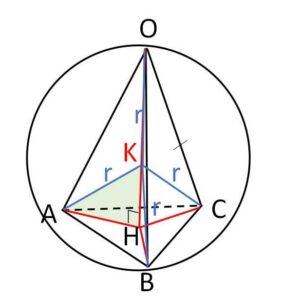
球の中心を\(K\)とする。\(KA=KB=KC\) より、\(K\)は直線\(OH\)(垂直二等分面の交線)上にあり、\(a≧1\) より\(K\)は線分\(OH\)上にある。・・・(補足)
よって直角三角形\(△KAH\)で三平方の定理より
\(r^2=(\displaystyle\frac{1}{\sqrt{3}})^2+(\sqrt{a^2-\displaystyle\frac{1}{3}}-r)^2\)
整理して
\(2r\sqrt{a^2-\displaystyle\frac{1}{3}}=a^2\)
したがって
\(r=\displaystyle\frac{a^2}{2\sqrt{a^2-\displaystyle\frac{1}{3}}}\)
(補足)条件 \(a≧1\) について
まず四面体が存在する条件(組み立てれるか)について考えると、\(O\)と\(H\)が重なるとき、\(a=\displaystyle\frac{1}{\sqrt{3}}\) となるので、\(a>\displaystyle\frac{1}{\sqrt{3}}\) は必要です(\(a\)の値が小さいと、線分\(OA,OB,OC\) が届かずに交わらないイメージ)。この条件は平方根の中身に現れています。
次に(3)の球の中心が線分\(OH\)上にある条件ですが、\(K\)が\(H\)と重なるときを考えて、\(OH=AH\) より
\(\sqrt{a^2-\displaystyle\frac{1}{3}}=\displaystyle\frac{1}{\sqrt{3}}\)
\(a=\sqrt{\displaystyle\frac{2}{3}}\)
となるので、\(a>\sqrt{\displaystyle\frac{2}{3}}\) が必要。\(a≧1\) は少し大きめにとっていますが、これらを満たしています。
(例題2)
半径\(r\)の球面上に4点\(A,B,C,D\)がある。四面体\(ABCD\)の各辺の長さは、\(AB=\sqrt{3}\)、\(AC=AD=BC=BD=CD=2\) を満たしている。このとき\(r\)の値を求めよ。
(解答)
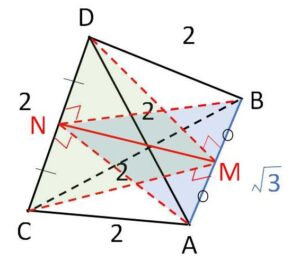
\(AB,CD\)の中点を\(M,N\)とおく。
まず線分\(AB\)の垂直二等分面について考えると
\(DM \perp AB\)、\(CM \perp AB\) と\(M\)が中点であることから、平面\(DMC\)は\(AB\)の垂直二等分面になる。
同様に平面\(ANB\)は線分\(CD\)の垂直二等分面になり、この2つの垂直二等分面の交線\(NM\)上に球の中心\(O\)がある。
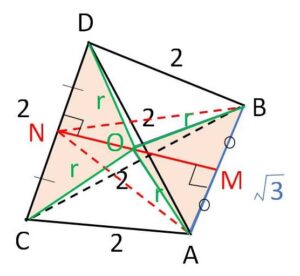
\(△OCD,△OAB\)は二等辺三角形なので、\(NM\)は\(CD,AB\)それぞれに垂直。よって三平方の定理より
\(NO=\sqrt{r^2-1^2}\)、\(OM=\sqrt{r^2-(\displaystyle\frac{\sqrt{3}}{2})^2}\)
また\(△NAB\)に着目すると
\(NM=\sqrt{(\sqrt{3})^2-(\displaystyle\frac{\sqrt{3}}{2})^2}=\displaystyle\frac{3}{2}\)
よって \(NO+OM=NM\) より
\(\sqrt{r^2-1}+\sqrt{r^2-\displaystyle\frac{3}{4}}=\displaystyle\frac{3}{2}\)
\(\sqrt{r^2-\displaystyle\frac{3}{4}}=\displaystyle\frac{3}{2}-\sqrt{r^2-1}\)
\(\displaystyle\frac{3}{2}-\sqrt{r^2-1}≧0\)・・・① であり
\(r^2-\displaystyle\frac{3}{4}=(\displaystyle\frac{3}{2}-\sqrt{r^2-1})^2\)
整理して
\(3\sqrt{r^2-1}=2\)
両辺\(0\)以上の値だから2乗して
\(9(r^2-1)=4\)
\(r^2=\displaystyle\frac{13}{9}\)
\(r=\displaystyle\frac{\sqrt{13}}{3}\) (①を満たす)
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
next→体積比 back→接する複数の球