三角比の相互関係

→高校数学TOP

三角比\(\sinθ,\cosθ,\tanθ\)にはどのような相互関係があるでしょうか。

・三角比の相互関係
半径1の半円の周上に点\(P(x,y)\)があるとき、\(\angle AOP=θ\) (\(0≦θ≦180°\)) とすると

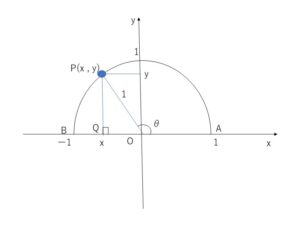
\(\sinθ=y\)・・・①
\(\cosθ=x\)・・・②
\(\tanθ=\displaystyle\frac{y}{x}\)・・・③

が成り立ちます。また三平方の定理より

\(x^2+y^2=1\)・・・④

が成り立ちます。(④は直角三角形\(OPQ\)ができない \((x,y)=(±1,0),(0,1)\) でも成り立つ。)

\(\cosθ≠0\) つまり \(θ≠90°\)のとき　①②を③に代入して
\(\tanθ=\displaystyle\frac{\sinθ}{\cosθ}\)・・・⑤

①②を④に代入すると
\(\sin^2θ+\cos^2θ=1\)・・・⑥

\(θ≠90°\)のとき  ⑥の両辺を\(\cos^2θ\)で割ると
\(1+\tan^2θ=\displaystyle\frac{1}{\cos^2θ}\)・・・⑦

⑤～⑦は超重要公式です。必ず覚えましょう。

(問題1)
\(0°≦θ≦180°\)　とする。
\(\sinθ=\displaystyle\frac{2}{5}\)　のとき、\(\cosθ,\tanθ\) の値を求めよ。

(解答)
\(\sin^2θ+\cos^2θ=1\) より　\(\cos^2θ=1-\sin^2θ\)
\(\cosθ=±\sqrt{1-\sin^2θ}=±\sqrt{1-\displaystyle\frac{4}{25}}=\)\(±\displaystyle\frac{\sqrt{21}}{5}\)

\(\tanθ=\displaystyle\frac{\sinθ}{\cosθ}=\displaystyle\frac{2}{5}÷(±\displaystyle\frac{\sqrt{21}}{5})=\)\(±\displaystyle\frac{2}{\sqrt{21}}\)