\(\sinθ=\displaystyle\frac{\sqrt{3}}{2}\) のように\(θ\)を未知の角とすれば、これは方程式とみることができます。この例のように未知の角の三角比を含む等式を三角方程式といい、この未知の角を求めることを三角方程式を解くといいます。
・三角方程式の解き方
三角方程式の解き方を例題を通してみていきます。ポイントは直線と単位円の交点です。
(例題1) \(0°≦θ≦180°\) のとき次の方程式を解け。
\(\sinθ=\displaystyle\frac{\sqrt{2}}{2}\)
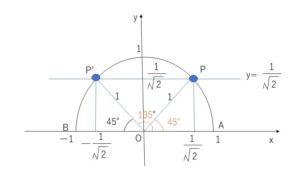
単位円を考えると,角\(θ\)における単位円上の点\(P\)の\(y\)座標が\(\sinθ\)です。なので\(y\)座標が\(\displaystyle\frac{\sqrt{2}}{2}\)の単位円上の点\(P\)を調べればよいので、直線 \(y=\displaystyle\frac{\sqrt{2}}{2} \) と単位円の交点を探します。あとは図形的に\(θ\)を求めます。
(解答)
単位円と\(y=\displaystyle\frac{\sqrt{2}}{2}=\displaystyle\frac{1}{\sqrt{2}}\)の交点は、点\(P,P’\)の2点。斜辺が\(1\)、高さが\(\displaystyle\frac{1}{\sqrt{2}}\)の直角三角形より、\(\angle AOP=\angle BOP’=45°\)よって図より、\(θ=45°,135°\)
単位円と\(y=\displaystyle\frac{\sqrt{2}}{2}=\displaystyle\frac{1}{\sqrt{2}}\)の交点は、点\(P,P’\)の2点。斜辺が\(1\)、高さが\(\displaystyle\frac{1}{\sqrt{2}}\)の直角三角形より、\(\angle AOP=\angle BOP’=45°\)よって図より、\(θ=45°,135°\)
(例題2) \(0°≦θ≦180°\) のとき次の方程式を解け。
\(\cosθ=-\displaystyle\frac{1}{2}\)
\(\cosθ=-\displaystyle\frac{1}{2}\)
今度は、単位円上の点\(P(\cosθ,\sinθ)\)で\(x\)座標が\(-\displaystyle\frac{1}{2}\)であるものを調べるため、
\(x=-\displaystyle\frac{1}{2}\)と単位円の交点を探します。
\(x=-\displaystyle\frac{1}{2}\)と単位円の交点を探します。
(解答)
単位円と直線\(x=-\displaystyle\frac{1}{2}\) の交点は\(P\)の1点。
斜辺が\(1\)、底辺が\(\displaystyle\frac{1}{2}\)の直角三角形から、\(\angle BOP=60°\)
よって \(θ=120°\)
単位円と直線\(x=-\displaystyle\frac{1}{2}\) の交点は\(P\)の1点。
斜辺が\(1\)、底辺が\(\displaystyle\frac{1}{2}\)の直角三角形から、\(\angle BOP=60°\)
よって \(θ=120°\)

(例題3) \(0°≦θ≦180°\) のとき次の方程式を解け。
\(\tanθ=-\displaystyle\frac{1}{\sqrt{3}}\)
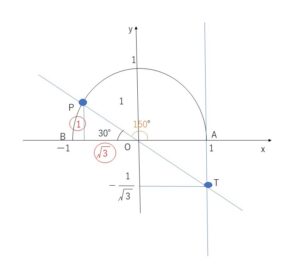
原点と単位円上の点\(P\)を結ぶ直線\(OP\)と直線\(x=1\)の交点を\(T(1,m)\)とすると、
\(\tanθ=\displaystyle\frac{y}{x}=\displaystyle\frac{m}{1}=m\) です。
よって、\(m=-\displaystyle\frac{1}{\sqrt{3}}\)から、\(T(1,-\displaystyle\frac{1}{\sqrt{3}})\)となり、\(OP\)上に\(T\)があることから、\(OT\)上に\(P\)があり、なおかつ\(P\)は単位円上の点なので、直線\(OT\)と単位円の交点を探せばよいことが分かります。あとは図形的に\(θ\)を求めます。
\(\tanθ=\displaystyle\frac{y}{x}=\displaystyle\frac{m}{1}=m\) です。
よって、\(m=-\displaystyle\frac{1}{\sqrt{3}}\)から、\(T(1,-\displaystyle\frac{1}{\sqrt{3}})\)となり、\(OP\)上に\(T\)があることから、\(OT\)上に\(P\)があり、なおかつ\(P\)は単位円上の点なので、直線\(OT\)と単位円の交点を探せばよいことが分かります。あとは図形的に\(θ\)を求めます。
(解答)
\(T(1,-\displaystyle\frac{1}{\sqrt{3}})\)とすると、直線\(OT\)と単位円の交点は\(P\)の1点。底辺と高さの比が \(1:\displaystyle\frac{1}{\sqrt{3}}=\sqrt{3}:1\) の直角三角形を考えると、\(\angle BOP=30°\)
よって、\(θ=150°\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。