係数が三角比の2次方程式の問題について解いていきます。\(x\)、\(θ\)の両方が登場しますが、やることは2次方程式の解の配置の問題を解く事とほとんど一緒です。
(問題)
\(0°≦θ≦180°\)とする \(x\)の2次方程式 \(3x^2+8x\cosθ+8\sinθ=0\) について、正の解だけをもつような\(θ\)の範囲を求めよ。
文字が\(x,θ\)の2つありますが、\(x\)の2次方程式なので\(x\)の2次関数のグラフを考えます(\(θ\)は定数とみます)。
①判別式 ②軸 ③端点 の3つに着目です。
①判別式 ②軸 ③端点 の3つに着目です。
(解答)
\(y=f(x)=3x^2+(8\cosθ)x+8\sinθ\) とおく。\(f(x)=0\)が正の解だけをもつ条件は、\(y=f(x)\)のグラフが下に凸の放物線であるので
\(y=f(x)=3x^2+(8\cosθ)x+8\sinθ\) とおく。\(f(x)=0\)が正の解だけをもつ条件は、\(y=f(x)\)のグラフが下に凸の放物線であるので
(1)判別式 \(D≧0\)
(2)軸\(>0\)
(3)\(f(0)>0\)
(2)軸\(>0\)
(3)\(f(0)>0\)
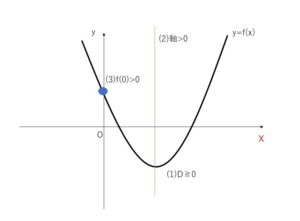
正の解を1つだけもつ場合も適するので、判別式の不等号にイコールをつけます。
(1)
\(\displaystyle\frac{D}{4}=(4\cosθ)^2-24\sinθ≧0\)
整理すると
\(2\sin^2θ+3\sinθ-2≦0\) となり
\((\sinθ+2)(2\sinθ-1)≦0\)
\(\sinθ+2>0\) より \(2\sinθ-1≦0\)
つまり、\(\sinθ≦\displaystyle\frac{1}{2}\)
\(0°≦θ≦180°\) だから、
\(0°≦θ≦30°\) または \(150°≦θ≦180°\)・・・①
\(\displaystyle\frac{D}{4}=(4\cosθ)^2-24\sinθ≧0\)
整理すると
\(2\sin^2θ+3\sinθ-2≦0\) となり
\((\sinθ+2)(2\sinθ-1)≦0\)
\(\sinθ+2>0\) より \(2\sinθ-1≦0\)
つまり、\(\sinθ≦\displaystyle\frac{1}{2}\)
\(0°≦θ≦180°\) だから、
\(0°≦θ≦30°\) または \(150°≦θ≦180°\)・・・①
(2)
軸は \(x=-\displaystyle\frac{4}{3}\cosθ\) だから
\(-\displaystyle\frac{4}{3}\cosθ>0\)
よって、\(\cosθ<0\) より \(0°≦θ≦180°\) だから、
\(90°<θ≦180°\)・・・②
軸は \(x=-\displaystyle\frac{4}{3}\cosθ\) だから
\(-\displaystyle\frac{4}{3}\cosθ>0\)
よって、\(\cosθ<0\) より \(0°≦θ≦180°\) だから、
\(90°<θ≦180°\)・・・②
(3)
\(f(0)=8\sinθ>0\) だから
\(\sinθ>0\) \(0°≦θ≦180°\) より、
\(0°<θ<180°\)・・・③
\(f(0)=8\sinθ>0\) だから
\(\sinθ>0\) \(0°≦θ≦180°\) より、
\(0°<θ<180°\)・・・③
①②③の共通部分が求める\(θ\)の範囲だから
\(150°≦θ<180°\)
\(150°≦θ<180°\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。