(問題)
\(AB=3,AC=2,\angle BAC=60°\) の\(△ABC\)において、\(\angle A\) の2等分線と\(BC\)の交点を\(D\)とするとき、線分\(AD\)の長さを求めよ。
(解答)面積を用いる方法
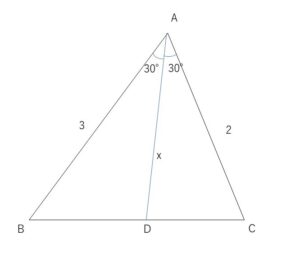
\(AD=x\)とする。
\(△ABC=\displaystyle\frac{1}{2}・3・2・\sin60°=\displaystyle\frac{3\sqrt{3}}{2}\) であり
\(△ABC=△ABD+△ACD=\displaystyle\frac{1}{2}・3・x・\sin30°+\displaystyle\frac{1}{2}・2・x・\sin30°\) だから
\(\displaystyle\frac{3\sqrt{3}}{2}=\displaystyle\frac{5}{4}x\)
したがって
\(AD=x=\displaystyle\frac{6\sqrt{3}}{5}\)
(解答2)余弦定理を用いる方法
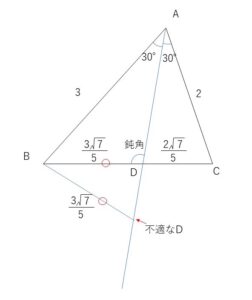
三角形\(ABC\)において余弦定理より
\(BC^2=3^2+2^2-2・3・2\cos60°\)
\(BC=7\) で\(BC>0\) より \(BC=\sqrt{7}\)
また、\(AD\)は角\(A\)の二等分線だから
\(BD:DC=3:2\) であり、\(BD=\displaystyle\frac{3\sqrt{7}}{5}\)
\(AD=x\) とおいて、三角形\(ABD\)において余弦定理より
\((\displaystyle\frac{3\sqrt{7}}{5})^2=3^2+x^2-2・3・x・\cos30°\)
整理すると
\(x^2-3\sqrt{3}+\displaystyle\frac{162}{25}=0\)
\((x-\displaystyle\frac{6\sqrt{3}}{5})(x-\displaystyle\frac{9\sqrt{3}}{5})=0\)
よって \(AD=x=\displaystyle\frac{6\sqrt{3}}{5},\displaystyle\frac{9\sqrt{3}}{5}\)
したがって、\(AD=\displaystyle\frac{6\sqrt{3}}{5}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。