円と内接四角形 | 教えて数学理科

円に内接する四角形についての問題を見ていきます。ポイントは内接四角形の対角の和が\(180°\)であることです。

(例題1)

円に内接している四角形\(ABCD\)において、\(AB=4,BC=2,CD=5,\angle BCD=120°\)であるとき、辺\(AD\)の長さを求めよ。

\(BD\)を結び、2つの三角形に分割します。
\(△BCD\)で余弦定理より\(BD\)の値を出し、次に\(△BAD\)で余弦定理を用いて\(AD\)の値を出します。内接四角形は対角の和が\(180°\)だから、\(\angle BAD=60°\)です。

(解答)

\(△BCD\)において余弦定理より
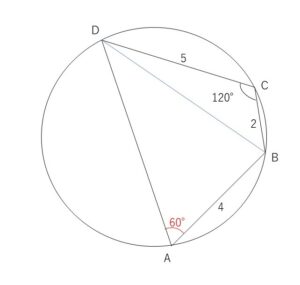
\(BD^2=5^2+2^2-2・5・2\cos120°\)
よって　\(BD^2=39\)・・・①

また、四角形\(ABCD\)は円に内接しているので
\(\angle BAD=180°-\angle BCD=60°\)

\(△BAD\)において余弦定理より
\(BD^2=AD^2+4^2-2・AD・4・\cos60°\)

①を代入して整理すると
\(AD^2-4AD-23=0\)
よって\(AD=2±3\sqrt{3}\) であり、\(AD>0\)だから

\(AD=2+3\sqrt{3}\)

(例題2)
円に内接している四角形\(ABCD\)において、\(AB=4,BC=4,CD=6,DA=10\)であるとき、四角形\(ABCD\)の面積\(S\)を求めよ。

例えば\(CA\)を結び2つの三角形に分割すると、\(\sin B\)が分かれば対角の\(\sin D\)も(対角の和が\(180°\)から)分かるので、\(\sin B\)を求めるために余弦定理より\(\cos B\)を求めます。\(CA\)の長さが分からないので未知数が2つになりますが、2つの三角形それぞれ余弦定理を用いることで連立して\(\cos B\)を求めます。

(解答)

四角形\(ABCD\)は円に内接しているので、\(D=180°-B\)
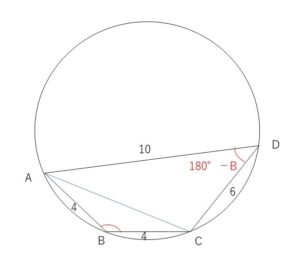
よって、\(\cos D=\cos(180°-B)=-\cos B\)

\(△ABC\)と\(△ADC\)にそれぞれ余弦定理を用いると

\(AC^2=4^2+4^2-2・4・4\cos B\)・・・①
\(AC^2=6^2+10^2-2・6・10(-\cos B)\)・・・②

②－①より
\(0=104+152\cos B\)　だから
\(\cos B=-\displaystyle\frac{13}{19}\)
\(0°<B<180°\) だから
\(\sin B=\sqrt{1-(-\displaystyle\frac{13}{19})^2}=\displaystyle\frac{\sqrt{192}}{19}=\displaystyle\frac{8\sqrt{3}}{19}\)

\(\sin D=\sin(180°-B)=\sin B\)だから

\(S=\displaystyle\frac{1}{2}・4・4・\sin B+\displaystyle\frac{1}{2}・6・10・\sin D\)
\(=\displaystyle\frac{1}{2}(16+60)・\displaystyle\frac{8\sqrt{3}}{19}\)
\(=\)\(16\sqrt{3}\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。

→高校数学TOP　next→角の二等分線と面積　 back→三角形と円