空間図形上での距離(移動距離)は、空間図形のままでは考えにくい場合、空間図形の展開図(平面図形)について考えると分かりやすいです。
(問題)
下の図のように、底面の直径\(AB\)が\(10\)、母線の長さ\(OA\)が\(30\)の直円錐がある。母線\(OA\)上に\(OC=10\)となるように点\(C\)をとる。点\(C\)から直円錐の側面を1巻きして、点\(A\)まで糸を張るとき、糸の長さの最小値を求めよ。
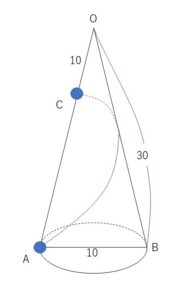
空間のままでは曲がっていたりと考えにくいので、展開図にして平面図形として考えます。展開図において\(C\)から\(A\)に行く経路はいろいろありますが、最も長さが短い経路は\(AC\)を直線で結んだときの線分\(AC\)です。展開図における経路の長さは立体を組み立てても変わらないので、線分\(AC\)の長さが求める糸の長さの最小値となります。
(解答)
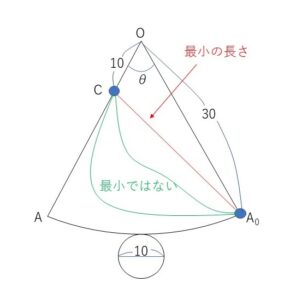
展開図を考えると、糸の長さの最小値は図の線分\(CA_0\)である。
ここで扇形の中心角を\(θ\)とすると
\(10π=30・2×π×\displaystyle\frac{θ}{360°}\) だから
\(θ=60°\)
よって、三角形\(OCA_0\)で余弦定理より
\(CA_0^2=10^2+30^2-2・10・30・\cos60°\)
\(CA_0^2=700\) で \(CA_0>0\) だから
\(CA_0=\sqrt{700}=\)\(10\sqrt{7}\)
以上になります。 お疲れさまでした。
ここまで見て頂きありがとうございました。
→高校数学TOP next→正四面体と球 back→空間図形の測量