集合の考え方をもとに、集合の要素の個数の数え方について見ていきます。
まずは、2つの集合の場合からです。
・有限集合と無限集合
集合\(P\)を1桁の自然数の集合、集合\(Q\)を正の数である3の倍数の集合とすると
\(P=\{1,2,3,4,\)\(5,6,7,8,9\}\)
\(Q=\{3,6,9,12・・・\}\)
となります。集合\(P\)の要素の個数は9個で有限ですが、集合\(Q\)の要素の個数は無限に多くあります。このように要素の個数が有限個である集合を有限集合、要素の個数が無限にある集合を無限集合といいます。有限集合である\(A\)について要素の個数を\(n(A\))と表すと、上の\(P\)については \(n(P)=9\) です。また、空集合は要素をもたないので \(n(φ)=0\) となります。
・和集合の要素の個数(2つの集合)
2つの集合\(A,B\)の和集合の要素の個数は、\(n(A),n(B)\)を用いてどのように表されるでしょうか。
ベン図を描くと次の通りになります。
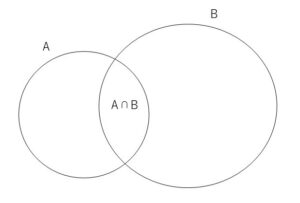
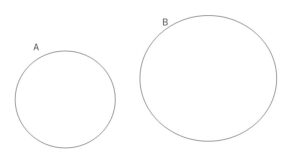
アンケートの例だと、アメリカとイギリスの両方に行ったことがある人がいない場合です。この場合は単純に アメリカ または イギリス に行ったことがある人は 10+10=20人 となります。
・補集合の要素の個数
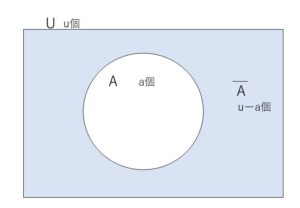
全体集合を\(U\)として、\(U\)の部分集合\(A\)と補集合\(\overline{A}\)を考えます。\(n(U)=u\)、\(n(A)=a\) とすると、\(n(\overline {A})=u-a\) だから
\(n(\overline {A})=n(U)-n(A)\)
が成り立ちます。
全体集合\(U\)とその部分集合\(A,B\)をベン図で表したときに、各領域で表される集合は次の通りになります。
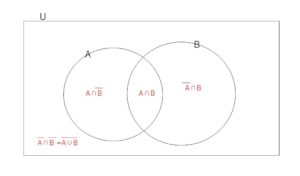
1題、例題をやってみます。
(例題)
100人の学生について、数学が「好きか、好きでないか」および「得意か得意でないか」について調べた。好きと答えた者は43人、得意と答えた者は29人、好きでもなく得意でもないと答えた者は35人であった。
(1)数学が好きであり、得意でもあると答えた者は何人か。
(2)数学が好きだが、得意ではないと答えた者は何人か。
(解答)
(1)
学生全体の集合を\(U\)、数学が好きであると答えた者の集合を\(A\)、数学が得意であると答えた者の集合を\(B\)とする。
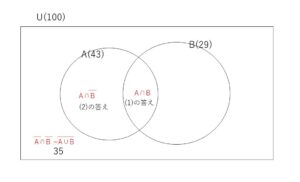
\(n(U)=100\), \(n(A)=43\), \(n(B)=29\), \(n(\overline A \cap \overline B)=35\) だから
\(n(A \cup B)=100-35=65\)
\(65=43+29-n(A \cap B)\)
求めるものは、\(n(A \cap \overline B)\) なので、図より
\(n(A \cap \overline B)\)\(=n(A)-n(A \cap B)=43-7=\)\(36(人)\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。