場合の数を求める簡単な計算方法について見ていきます。
・和の法則
次の問題について考えてみます。
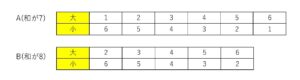
\(6+5=7\)(通り)
となります。
\(A\)の起こり方が\(m\)通り、\(B\)の起こり方が\(n\)通りとすれば、
\(A\)または\(B\)の起こる場合の数は \(m+n\) 通りあることになります。
これは、事柄\(A,B\)が起こる場合の全体を集合\(A,B\)とした場合、
\(n(A \cup B)\)\(=n(A)+n(B)-n(A \cap B)\)
で、\(A \cap B=φ\) に対応しています。
\(1\)から\(12\)までの数字を1つずつ書いたカードが12枚ある。この中から、2枚のカードを取り出すとき、数字の和が\(7\)の倍数になる場合の数を求めよ。
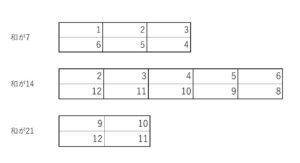
\(3+5+2=\)\(10\)(通り)
・積の法則
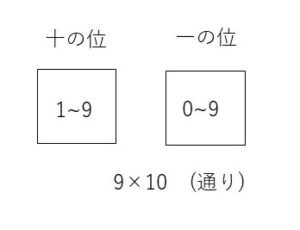
2桁の自然数の個数は、\(10\)から\(99\)までの自然数の個数なので、\(99-10+1\)\(=90\)(個) 存在します。これを各位の数字の取り方に着目して考えると、
十の位の数字の取り方は、\(1\)から\(9\)までの\(9\)通り
一の位の数字の取り方は、\(0\)から\(9\)までの\(10\)通り
であり、十の位の各々(おのおの)の数字に対して、一の位の数字が10通りあることになるので
2桁の自然数の個数\(=9×10=90\)(個) と積を計算することでも求めることができます。
一般に、2つの事柄\(A,B\)があって、\(A\)の起こり方が\(m\)通りあり、その各々に対して\(B\)の起こり方が\(n\)通りあるとき、\(A,B\)がともに起こる場合の数は \(mn\) 通りあることになります。
(例題2)
新聞が\(4\)種類、週刊誌が\(5\)種類、月刊雑誌が\(3\)種類ある。各種のものそれぞれ1つずつ選ぶには、何通りの選び方があるか。
(解答)
新聞\(1\)つに対して、週刊誌の選び方が\(5\)通り、さらに週刊誌\(1\)つに対して月刊雑誌の選び方が\(3\)通り。よって積の法則より
\(4×5×3=\)\(60\)(通り)
(例題3)
\((a+b+c)(x+y)^2\) を展開すると、何個の項の和になるか。
(解答)
\((a+b+c)(x+y)^2\)\(=(a+b+c)(x^2+2xy+y^2)\)
\((a+b+c)(x^2+2xy+y^2)\) を展開してできる項は
\((a,b,c)\), \((x^2,2xy,y^2)\) のそれぞれから1つずつ選んで掛けて作られるので
\(3×3=\)\(9\)(個)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。