順列の漸化式に関する問題について見ていきます。
(問題)
文字\(a\)と\(b\)をいくつか並べた列のうちで、\(b\)が隣り合わないものだけを考える。文字が\(n\)個並んだものを「長さ\(n\)の列」とよぶとき
(1)長さ\(3\)の列、長さ\(4\)の列はそれぞれ何通りあるか。
(2)長さ\(5\)の列で、\(a\)で始まる列は何通りあるか。また、長さ\(5\)の列で、\(b\)で始まる列は何通りあるか。
(3)長さ\(n\)の列の個数を\(f(n)\)とするとき、\(f(n+2)=\)\(f(n+1)+f(n)\)が成り立つことを示せ。
(解答)
(1)
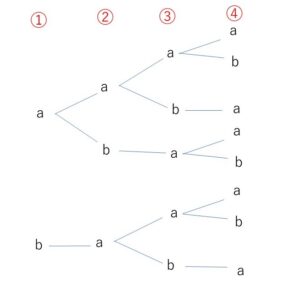
具体的に列を書き上げて数えます。
樹形図より、長さ\(3\)の列は、
\(aaa\), \(aab\), \(aba\), \(baa\), \(bab\) の\(5\)通り
\(aaa\), \(aab\), \(aba\), \(baa\), \(bab\) の\(5\)通り
長さ\(4\)の列は、
\(aaaa\), \(aaab\), \(aaba\), \(abaa\), \(abab\), \(baaa\), \(baab\), \(baba\) の\(8\)通り
\(aaaa\), \(aaab\), \(aaba\), \(abaa\), \(abab\), \(baaa\), \(baab\), \(baba\) の\(8\)通り
(2)
そのまま樹形図を書けば答えは出ますが、(3)を意識して解きます。
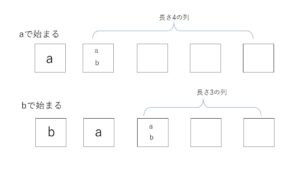
まず先頭の文字が\(a\)の場合は、2文字目は\(a,b\)どちらでもよく、2,3,4,5文字目で\(b\)が連続して並ばない場合は、(1)での長さ\(4\)の列の場合だけあるので、先頭の文字が\(a\)の長さ\(5\)の列は、長さ\(4\)の列の数だけあります。
先頭が\(b\)の場合は、2文字目が\(a\)でなければならず、3文字目は\(a,b\)問わないので、3,4,5文字目で\(b\)が並ばない場合の数、つまり長さ\(3\)の列の数だけあります。
まず先頭の文字が\(a\)の場合は、2文字目は\(a,b\)どちらでもよく、2,3,4,5文字目で\(b\)が連続して並ばない場合は、(1)での長さ\(4\)の列の場合だけあるので、先頭の文字が\(a\)の長さ\(5\)の列は、長さ\(4\)の列の数だけあります。
先頭が\(b\)の場合は、2文字目が\(a\)でなければならず、3文字目は\(a,b\)問わないので、3,4,5文字目で\(b\)が並ばない場合の数、つまり長さ\(3\)の列の数だけあります。

\(a\)で始まる列は、長さ\(4\)の列の頭に\(a\)をつければよいので、\(8\)(通り)
\(b\)で始まる列は、長さ\(3\)の列の頭に\(ba\)をつければよいので、\(5\)(通り)
(3)
(2)の解法は、(3)の漸化式に\(n=3\)を代入したものになります。
\(f(5)=f(4)+f(3)\)
これを一般的な場合について同じように考えればよいです。
\(f(5)=f(4)+f(3)\)
これを一般的な場合について同じように考えればよいです。
長さ\((n+2)\)の列は、\(a\)で始まる列と\(b\)で始まる列に分けられる。
\(a\)で始まる列は、長さ\((n+1)\)の列に\(a\)をつけ、
\(b\)で始まる列は、長さ\(n\)の列に\(ba\)をつければよいので
\(f(n+2)\)\(=f(n+1)+f(n)\) が成り立つ。
\(a\)で始まる列は、長さ\((n+1)\)の列に\(a\)をつけ、
\(b\)で始まる列は、長さ\(n\)の列に\(ba\)をつければよいので
\(f(n+2)\)\(=f(n+1)+f(n)\) が成り立つ。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。