(例題)
\(1\)から\(n\)までの番号がついている箱とボールがあって、1つの箱に1個のボールを入れるものとする。箱の番号とボールの番号がすべて異なる入れ方の個数を\(W(n)\)と表すとき、\(W(1)=0\),\(W(2)=1\),\(W(3)=(ア)\),\(W(4)=(イ)\)である。
\(n=1\)のとき順列は\(1\)の1通りしかないので、ボールと箱の番号が一致するため、\(W(1)=0\)、
\(n=2\)のときは順列は\(12\)か\(21\)で、ボールと箱の番号が一致しないのは\(21\)の1通りなので\(W(2)=1\)です。
以下同様に、\(n=3,4\)の場合は全部の場合を考えてもそこまで大変ではないので、すべて書き上げて数えてきます。先頭のボールの番号が1ではないことに着目します。
箱を左から順に\(1,2,3・・・\)と並べて、それに対するボールの番号の順列を考える。
(ア)
\(n=3\)のとき
条件を満たす順列は、\(231\),\(312\)の2通り。よって、\(W(3)=2\)
\(n=4\)のとき
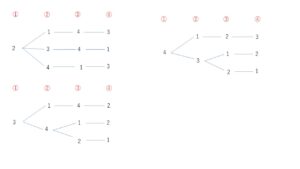
条件を満たす順列は、樹形図より
\(2143\), \(2341\), \(2413\)
\(3142\), \(3412\), \(3421\)
\(4123\), \(4312\), \(4321\) の9通り。
よって、\(W(4)=9\)
5個の数字の完全順列の総数\(W(5)\)は上の例題の解答のように樹形図で数えることもできますが、個数\(n\)での総数を求める準備のために、次のように求めてみます。
4個の数字の順列には、\(k\)番目に数字\(k\)がくる回数が
0回(完全順列)、1回、2回、4回の場合があります。
(3回の場合は4つめの数字も順番と一致することになるのでありえない)
このうち先ほどの入れ替えの方式で5個の完全順列を作るには、0回と1回のときでしか作れません。よってこの2パターンを考えると
①4個の順列が完全順列の場合
数字5を1~4番目のどの数字と入れ替えても5個の完全順列ができる。
②4個の順列で1回だけ順番と数字が一致するとき
その一致する数字と数字5を入れ替えれば5個の完全順列ができる。
①4個の完全順列の個数は\(W(4)\)です。
②4個の順列で1回だけ順番と数字が一致する個数は、例えば3番目に数字3がくるとしたら、\(1,2,4\)番目にそれぞれ数字\(1,2,4\)がこない場合の数で、これは3個の順列を考えたとき、\(1,2,3\)番目にそれぞれ数字\(1,2,3\)がこない場合の数と同じことなので、3個の完全順列の個数と同じになります。
①の場合は、1~4番目の4通り入れ替え方があり、②の場合は順番と数字が一致する場合が1~4番目の4通りあるので、\(W(5)\)を\(W(4),W(3)\)で表すと
\(W(5)=4W(4)+4W(3)\)\(=4\{W(4)+W(3)\}\)・・・(A)
となります。
例題の答えを用いると、\(W(5)=4(9+2)=44\) です。
\(n\)個の数字の完全順列の総数\(W(n)\)は同じように考えると、(A)の式の 5→\(n\)、4→\(n-1\)、3→\(n-2\) とすればよいので
\(W(n)=(n-1)\{W(n-1)+W(n-2)\}\)・・・(B)
となります。
・完全順列の総数(一般項)
では(B)式(漸化式)を解いて\(W(n)\)の一般項を求めてみます。
\(W(n)=a_n\) として見慣れた形にしておきます。
\(a_{n}=(n-1)\{a_{n-1}+a_{n-2}\}\)・・・(C)
\(a_1=0,a_2=1\)
(C)を変形すると
\(a_{n}-na_{n-1}\)\(=-\{a_{n-1}-(n-1)a_{n-2}\}\)・・・(D)
\(a_{n}+(pn+q)a_{n-1}\)\(=r\{a_{n-1}+(p(n-1)+q)a_{n-1}\}\)
とおいて、(C)と係数比較することで、\(p=-1,q=0,r=-1\) より(D)が導かれます。
\(a_{n}-na_{n-1}=b_n\) ・・・(E) とおくと (D)は
\(b_n=-b_{n-1}\) で
\(b_n=(-1)^{n-2}b_2\)\(=(-1)^{n-2}(a_2-2a_1)\)\(=(-1)^{n-2}\)
\((-1)^{n-2}=(-1)^{n-2}×(-1)^2=(-1)^n\) だから (E)より
\(a_{n}-na_{n-1}=\)\((-1)^n\) であり
\(a_{n}=na_{n-1}+(-1)^n\)
両辺 \(n!\) で割ると
\(\displaystyle\frac{a_n}{n!}=\displaystyle\frac{a_{n-1}}{(n-1)!}+\displaystyle\frac{(-1)^n}{n!}\)・・・(F)
\(\displaystyle\frac{a_n}{n!}=c_n\)・・・(G) とおくと(F)は
\(c_n=c_{n-1}+\displaystyle\frac{(-1)^n}{n!}\)
\(n≧2\)のとき
\(c_n=c_1+\displaystyle\sum_{k=2}^n \displaystyle\frac{(-1)^k}{k!}\)\(=\displaystyle\sum_{k=2}^n \displaystyle\frac{(-1)^k}{k!}\) \((∵c_1=0)\)
よって (G)より
\(\displaystyle\frac{a_n}{n!}\)\(=\displaystyle\sum_{k=2}^n \displaystyle\frac{(-1)^k}{k!}\) となるから
\(W(n)=n!\displaystyle\sum_{k=2}^n \displaystyle\frac{(-1)^k}{k!}\) (\(n≧2\))
\(W(1)=0\)
なお、\(\displaystyle\frac{(-1)^k}{k!}\)は
\(k=0\) のとき \(\displaystyle\frac{(-1)^0}{0!}=1\)
\(k=1\) のとき \(\displaystyle\frac{(-1)^1}{1!}=-1\)
だから、\(W(n)\)を次のように表すと\(n=1\)でも成り立ちます。
\(W(n)=n!\displaystyle\sum_{k=0}^n \displaystyle\frac{(-1)^k}{k!}\) (\(n≧1\))
後半はかなりハイレベルな内容です。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。