正多角形の頂点を3つ選んでできる三角形で、正三角形などの特殊な三角形がいくつできるか数える問題について考えていきます。
(例題)
正\(n\)角形がある(\(n\)は\(3\)以上の整数)。この正\(n\)角形の\(n\)個の頂点のうち\(3\)個を頂点とする三角形について考える。
(1)\(n=6\)とする。このとき、三角形は全部で(ア)個あり、直角三角形は(イ)個ある。また、二等辺三角形は(ウ)個あり、そのうち正三角形は(エ)個ある。
(2)\(n=8\)とする。このとき、直角三角形は(オ)個、鈍角三角形は(カ)個、鋭角三角形は(キ)個ある。
(3)\(n=6k\)(\(k\)は正の整数)であるとする。このとき、\(k\)を用いて表すと、正三角形の個数は(ク)であり、直角三角形の個数は(ケ)である。
正\(n\)角形を図示する際には、円を書き、弧と弦の長さは比例するので 同じ長さの弧に対応する弦の長さは等しいので、円周を\(n\)個に分割する点を頂点として図示します。
なお、(1)(2)は\(n\)が具体的な数字ですが、(3)のような一般的な正\(n\)角形の場合にも応用できるように解答を作ってあります。
なお、(1)(2)は\(n\)が具体的な数字ですが、(3)のような一般的な正\(n\)角形の場合にも応用できるように解答を作ってあります。
(解答)
(1)
(ア)
\(6\)個の頂点のうち\(3個\)を選んで結べば三角形ができるので、
(1)
(ア)
\(6\)個の頂点のうち\(3個\)を選んで結べば三角形ができるので、
\({}_6\mathrm{C}_3=\)\(20\)(個)
(イ)
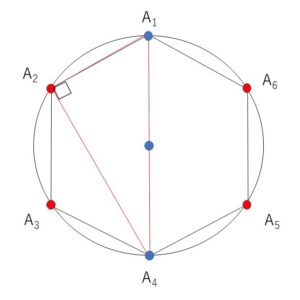
円の直径を三角形の1辺(斜辺)とすると、直径の両端の点以外の頂点を1つ選べば、直角三角形ができます。(円周角が90°を利用)
中心を通る正六角形の対角線の本数を数えることになりますが、1つの頂点につき一本あり、6本とすると1本の対角線を2回重複して数えていることになるので、6÷2 本です。
中心を通る正六角形の対角線の本数を数えることになりますが、1つの頂点につき一本あり、6本とすると1本の対角線を2回重複して数えていることになるので、6÷2 本です。
外接円の中心を通る正六角形の対角線は全部で、\(6÷2=3\)(本)
このうち例えば頂点\(A_1,A_4\)を結ぶ対角線について考えると、この対角線を斜辺として、残り4点\(A_2,A_3,\)\(A_5,A_6\) から1点を三角形の頂点として選べば直角三角形ができる。他の\(A_2,A_5\)と\(A_3,A_6\)を結ぶ対角線でも同様に考えて、
\(3×4=\)\(12\)(個)
\(3×4=\)\(12\)(個)
(ウ)
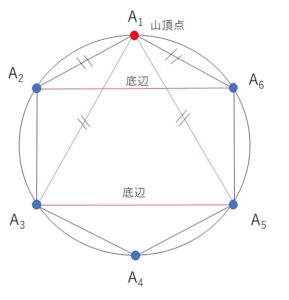
二等辺三角形(正三角形も含む)を作るには、まず1点を二等辺三角形の等しい2辺の交点(山頂点)として選びます。
例えば\(A_1\)を山頂点として選ぶと、等しい2辺以外の辺(底辺)を\(A_2-A_6\)、\(A_3-A_5\)としてやれば二等辺三角形ができ、他の\(A_2~A_6\)でも同様です(2×6=12個)。ただし正三角形でない二等辺三角形についてはそれぞれ別の三角形となりますが、正三角形の場合にはすべての辺が等しいため、底辺と山頂点が区別できず、他の辺や頂点が底辺や山頂点になりうるので、この数え方だと正三角形を重複して数えていることになります。(\(A_1\)を山頂点、底辺を\(A_3-A_5\)とする正三角形と、\(A_3\)を山頂点、底辺を\(A_5-A_1\)とする正三角形と、\(A_5\)を山頂点、底辺を\(A_1-A_3\)とする正三角形は同じもの)
今回は問題に(エ)で正三角形の個数が聞かれているので分けて考えるのは分かると思いますが、(ウ)単体のみで聞かれているときも分けて考えるか、重複分を調整するようにしてください。
例えば\(A_1\)を山頂点として選ぶと、等しい2辺以外の辺(底辺)を\(A_2-A_6\)、\(A_3-A_5\)としてやれば二等辺三角形ができ、他の\(A_2~A_6\)でも同様です(2×6=12個)。ただし正三角形でない二等辺三角形についてはそれぞれ別の三角形となりますが、正三角形の場合にはすべての辺が等しいため、底辺と山頂点が区別できず、他の辺や頂点が底辺や山頂点になりうるので、この数え方だと正三角形を重複して数えていることになります。(\(A_1\)を山頂点、底辺を\(A_3-A_5\)とする正三角形と、\(A_3\)を山頂点、底辺を\(A_5-A_1\)とする正三角形と、\(A_5\)を山頂点、底辺を\(A_1-A_3\)とする正三角形は同じもの)

今回は問題に(エ)で正三角形の個数が聞かれているので分けて考えるのは分かると思いますが、(ウ)単体のみで聞かれているときも分けて考えるか、重複分を調整するようにしてください。
まず、二等辺三角形のうち正三角形でないものを数える。
1点を二等辺三角形の等しい2辺の交点(頂点)として選ぶと、その選び方は6通り。
そのうち\(A_1\)を頂点とすると、\(A_2,A_6\)を選べば二等辺三角形ができる。
他の\(A_2~A_6\)を頂点として選ぶ場合も同様に考えると
\(1×6=6\)(個)
1点を二等辺三角形の等しい2辺の交点(頂点)として選ぶと、その選び方は6通り。
そのうち\(A_1\)を頂点とすると、\(A_2,A_6\)を選べば二等辺三角形ができる。
他の\(A_2~A_6\)を頂点として選ぶ場合も同様に考えると
\(1×6=6\)(個)
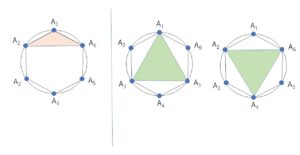
次に、正三角形は、\((A_1,A_3,A_5)\)と\((A_2,A_4,A_6)\)を頂点として選べばできるので、\(2\)(個)
よって
(ウ)は、\(6+2=\)\(8\)(個)
(エ)は、\(2\)(個)
(エ)は、\(2\)(個)
(2)
(オ)直角三角形の個数は(1)の(イ)と同じように数えます。
(オ)
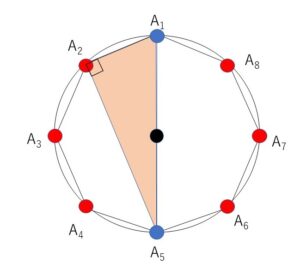
外接円の中心を通る正八角形の対角線は全部で、\(8÷2=4\)(本)
このうち例えば頂点\(A_1,A_5\)を結ぶ対角線について考えると、この対角線を斜辺として、残り6点\(A_2,A_3,A_4,\)\(A_6,A_7,A_8\) から1点を三角形の頂点として選べば直角三角形ができる。他の3本の対角線でも同様に考えて、
\(4×6=\)\(24\)(個)
\(4×6=\)\(24\)(個)
(カ)
鈍角三角形についても円の中心を通る対角線(直径)に着目します。
まず、点\(A_1\)について、\(A_1\)から左周りに\(A_1\)を通る直径の端点\(A_5\)までたどって、間にある点\(A_2~A_4\)の3点から2点を選び、その2点と\(A_1\)を結んだ三角形を考えます。この三角形は図から(円周の半分より大きい弧に対応する円周角を1角とする三角形となる)90°より大きい角をもつ鈍角三角形となります。他の\(A_2~A_8\)でも同様です。
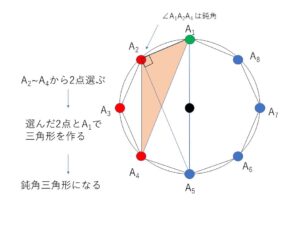
まず、点\(A_1\)について、\(A_1\)から左周りに\(A_1\)を通る直径の端点\(A_5\)までたどって、間にある点\(A_2~A_4\)の3点から2点を選び、その2点と\(A_1\)を結んだ三角形を考えます。この三角形は図から(円周の半分より大きい弧に対応する円周角を1角とする三角形となる)90°より大きい角をもつ鈍角三角形となります。他の\(A_2~A_8\)でも同様です。

正八角形の頂点1つ\(A_1\)に着目する。
\(A_1\)から左回りに\(A_1\)を通る直径の端点\(A_5\)までたどり、間の点\(A_2~A_4\)3点から2点を選び、その2点と\(A_1\)を結ぶと鈍角三角形ができる。
他の\(A_2~A_8\)でも同様に考えると、鈍角三角形は
\({}_3\mathrm{C}_2×8=\)\(24\)(個) できる。
\(A_1\)から左回りに\(A_1\)を通る直径の端点\(A_5\)までたどり、間の点\(A_2~A_4\)3点から2点を選び、その2点と\(A_1\)を結ぶと鈍角三角形ができる。
他の\(A_2~A_8\)でも同様に考えると、鈍角三角形は
\({}_3\mathrm{C}_2×8=\)\(24\)(個) できる。
(キ)
(オ),(カ)より、鋭角三角形ではないものは、\(24+24\)\(=48\)(個)
三角形は全部で、\({}_8\mathrm{C}_3=56\)(個)あるので
鋭角三角形は、\(56-48=\)\(8\)(個)
鋭角三角形は、\(56-48=\)\(8\)(個)
(3)
(1)の考え方をそのまま使います。
(ク)正三角形の個数について
(1)では頂点間の\(A\)の右下の数字の差が\(2\)(\(6÷3\))でしたが、正\(6k\)角形では\(6k÷3=2k\)となります。3で割るのは円周を3等分するからです。
(ク)正三角形の個数について
(1)では頂点間の\(A\)の右下の数字の差が\(2\)(\(6÷3\))でしたが、正\(6k\)角形では\(6k÷3=2k\)となります。3で割るのは円周を3等分するからです。
(ク)
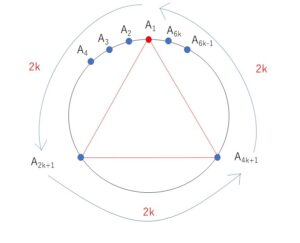
正\(n\)角形(正\(6k\)角形)の頂点を、\(A_1,A_2・・・A_n\) とする。
\(A_1\)を頂点とする正三角形の他の頂点は\(A_{2k+1},A_{4k+1}\) となる。
同様に、\((A_2,A_{2k+2},A_{4k+2})\),\((A_3,A_{2k+3},A_{4k+3})\)・・・\((A_{2k},A_{4k},A_{6k})\) を頂点とする正三角形があるので、全部で \(2k\) (個) ある。
正\(n\)角形(正\(6k\)角形)の頂点を、\(A_1,A_2・・・A_n\) とする。
\(A_1\)を頂点とする正三角形の他の頂点は\(A_{2k+1},A_{4k+1}\) となる。
同様に、\((A_2,A_{2k+2},A_{4k+2})\),\((A_3,A_{2k+3},A_{4k+3})\)・・・\((A_{2k},A_{4k},A_{6k})\) を頂点とする正三角形があるので、全部で \(2k\) (個) ある。
(ケ)
正\(6k\)角形の外接円の中心を通る対角線の本数は、\(6k÷2=3k\) (本)である。
そのうち1つの対角線をとりあげると、この対角線を斜辺として対角線の両端を除く\(6k-2\)(個)から頂点を1つ選び三角形を作ると直角三角形になる。
よって、直角三角形の総数は \(3k(6k-2)=\)\(6k(3k-1)\)(個)
そのうち1つの対角線をとりあげると、この対角線を斜辺として対角線の両端を除く\(6k-2\)(個)から頂点を1つ選び三角形を作ると直角三角形になる。
よって、直角三角形の総数は \(3k(6k-2)=\)\(6k(3k-1)\)(個)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。