図形と組合せに関する問題について考えていきます。
今回は、円に内接する多角形をテーマとした問題を扱っていきます。
(例題)
円に内接する\(n\)角形F(\(n>4)\)の対角線の総数は(ア)本である。また、Fの頂点3つからできる三角形の総数は(イ)個、Fの頂点4つからできる四角形の総数は(ウ)個である。さらに、対角線のうちどの3本をとってもFの頂点以外の同一点で交わらないとすると、Fの対角線の交点のうち、Fの内部で交わるものの総数は(エ)個である。
(解答)
(ア)
2点を選べば、2点を結ぶ直線が1つできます。\(n\)角形は頂点が\(n\)個なので、\({}_n\mathrm{C}_2\) を考えますが、このうち対角線にならない選び方があります。それは2点を結ぶ線分が\(n\)角形の辺になる場合です。
\(n\)個の頂点から、2個の点を選んで結んで線分をつくる。
そのうちFの辺になるものを除けばよいので、
\({}_n\mathrm{C}_2-n=\displaystyle\frac{n(n-1)}{2}-n=\)\(\displaystyle\frac{n(n-3)}{2}\)(本)
そのうちFの辺になるものを除けばよいので、
\({}_n\mathrm{C}_2-n=\displaystyle\frac{n(n-1)}{2}-n=\)\(\displaystyle\frac{n(n-3)}{2}\)(本)
(イ)(ウ)
3点を選べば三角形ができます。四角形についても同様に4点を選べばよいです。
\(n\)個の頂点から3点を選んで結べば三角形ができるので
\({}_n\mathrm{C}_3=\)\(\displaystyle\frac{n(n-1)(n-2)}{6}\) (個)
\({}_n\mathrm{C}_3=\)\(\displaystyle\frac{n(n-1)(n-2)}{6}\) (個)
また\(n\)個の頂点から4点を選んで結べば四角形ができるので
\({}_n\mathrm{C}_4=\)\(\displaystyle\frac{n(n-1)(n-2)(n-3)}{24}\) (個)
\({}_n\mathrm{C}_4=\)\(\displaystyle\frac{n(n-1)(n-2)(n-3)}{24}\) (個)
(エ)
(ウ)を利用します。
「Fの内部で交わる対角線2本を決めると、その対角線2本をもつ四角形が1つ決まります。」対角線2本とそれに対する四角形は1:1対応しているので、交点を数えるには、四角形を数えればよいことになります。
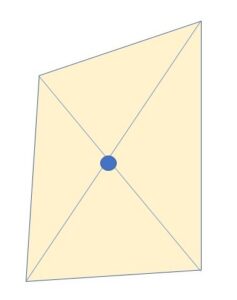
「」内が成り立つのは問題文の{対角線のうちどの3本をとってもFの頂点以外の同一点で交わらないとすると}という条件があるからです。これについては後程触れます。
「Fの内部で交わる対角線2本を決めると、その対角線2本をもつ四角形が1つ決まります。」対角線2本とそれに対する四角形は1:1対応しているので、交点を数えるには、四角形を数えればよいことになります。

「」内が成り立つのは問題文の{対角線のうちどの3本をとってもFの頂点以外の同一点で交わらないとすると}という条件があるからです。これについては後程触れます。
Fの内部で交わる対角線2本を決めると、その対角線2本をもつ四角形が1つ決まるので、求める交点の個数は(ウ)の四角形の個数と同じ。
\(\displaystyle\frac{n(n-1)(n-2)(n-3)}{24}\) (個)
{対角線のうちどの3本をとってもFの頂点以外の同一点で交わらないとすると}という条件がないと、「四角形の個数=内部にある対角線の交点の個数」とはなりません。例えば六角形で考えてみると、3本の対角線が内部で1点で交わるときは次の図のようになり、1個の内部にある対角線の交点につき、3個の四角形が対応することになります。
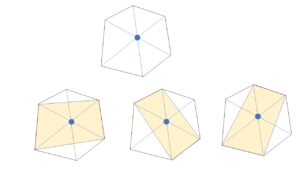

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
→高校数学TOP next→図形と組合せ③ back→同じものを含む円順列・じゅず順列