\(xy\)座標平面に関する確率の問題について見ていきます。
(例題1)
2つのさいころA,Bを投げて、Aの目の数を\(x\)座標、Bの目の数を\(y\)座標とする平面上の点を定める。この試行を3回続けて行って定める点を順にP,Q,Rとするとき、次の確率を求めよ。
(1)P,Q,Rが互いに異なる3点になる確率
(2)3点P,Q,Rが\(x\)軸に平行な直線上にある確率
(3)P,Q,Rが互いに異なり、かつ傾きが1の直線上にある確率
全事象を同様に確からしい状態にするために、P,Q,Rを区別します。
P(1,2) Q(3,4) R(4,2) と P(3,4) Q(4,2) R(1,2) は別のものとなります。
なお、1回の試行で \(x\)座標の決め方は6通り、\(y\)座標の決め方が6通りなので、36通りの場合があり、3回の試行では \(36^3\) 通りです。
36個の点を座標で表すと次の図のとおりです。
P(1,2) Q(3,4) R(4,2) と P(3,4) Q(4,2) R(1,2) は別のものとなります。
なお、1回の試行で \(x\)座標の決め方は6通り、\(y\)座標の決め方が6通りなので、36通りの場合があり、3回の試行では \(36^3\) 通りです。
36個の点を座標で表すと次の図のとおりです。

(解答)
(1)
Pの選び方は36通りです。Qの選び方はP以外の35通り、Rの選び方はP,Q以外の34通りです。つまり36個から3個とる順列を考えることになります。
おこりうるすべての場合の数は、\(36^3\) 通り。
このうちP,Q,Rが異なる3点になる場合の数は
\(36×35×34\) 通り。よって求める確率は
\(\displaystyle\frac{36×35×34}{36^3}=\)\(\displaystyle\frac{595}{648}\)
(2)
Pの選び方36通りに対して、Q,Rは\(y\)座標はPと同じで\(x\)座標はなんでもよいのでそれぞれ6通りあります。
P,Q,Rは異なる点でなくてもよいことに注意してください。
P,Q,Rは異なる点でなくてもよいことに注意してください。
Pの選び方36通りに対して、Q,RはPと\(y\)座標が同じで\(x\)座標はどれでもよいので、求める確率は
\(\displaystyle\frac{36×6×6}{36^3}=\)\(\displaystyle\frac{1}{36}\)
\(\displaystyle\frac{36×6×6}{36^3}=\)\(\displaystyle\frac{1}{36}\)
(3)
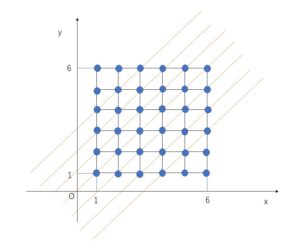
条件に合う直線は、\(y=x\), \(y=x±1\), \(y=x±2\), \(y=x±3\) の計7本です。
例えば\(y=x\)上の6点からP,Q,Rを決めるとき、(1)と同様で、Pの選び方が6通り、Qの選び方がP以外の5通り、Rの選び方がP,Q以外の4通りとなるで、全部で \({}_6\mathrm{P}_3\) 通りです。
例えば\(y=x\)上の6点からP,Q,Rを決めるとき、(1)と同様で、Pの選び方が6通り、Qの選び方がP以外の5通り、Rの選び方がP,Q以外の4通りとなるで、全部で \({}_6\mathrm{P}_3\) 通りです。
条件に合う直線は、\(y=x\), \(y=x±1\), \(y=x±2\), \(y=x±3\) の計7本。
またそれぞれの直線に点が、6,5,4,3 個ある。
P,Q,Rが異なるので、それぞれの直線でのP,Q,Rの選び方は、\({}_6\mathrm{P}_3\), \({}_5\mathrm{P}_3\), \({}_4\mathrm{P}_3\), \({}_3\mathrm{P}_3\) 通り。
よって求める確率は
\(\displaystyle\frac{{}_6\mathrm{P}_3+2({}_5\mathrm{P}_3+{}_4\mathrm{P}_3+{}_3\mathrm{P}_3)}{36^3}=\)\(\displaystyle\frac{25}{3888}\)
またそれぞれの直線に点が、6,5,4,3 個ある。
P,Q,Rが異なるので、それぞれの直線でのP,Q,Rの選び方は、\({}_6\mathrm{P}_3\), \({}_5\mathrm{P}_3\), \({}_4\mathrm{P}_3\), \({}_3\mathrm{P}_3\) 通り。
よって求める確率は
\(\displaystyle\frac{{}_6\mathrm{P}_3+2({}_5\mathrm{P}_3+{}_4\mathrm{P}_3+{}_3\mathrm{P}_3)}{36^3}=\)\(\displaystyle\frac{25}{3888}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。