ド・モルガンの法則やベン図を利用した確率の問題について見ていきます。
まずはド・モルガンの法則のおさらいです。
(ド・モルガンの法則)
①\(\overline{A \cap B}\)\(=\overline{A} \cup \overline{B}\)
②\(\overline{A \cup B}\)\(=\overline{A} \cap \overline{B}\)
①\(\overline{A \cap B}\)\(=\overline{A} \cup \overline{B}\)
②\(\overline{A \cup B}\)\(=\overline{A} \cap \overline{B}\)
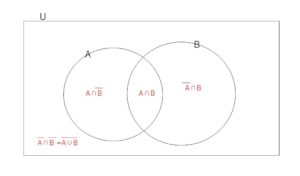
また、次の図より全事象\(U\)は、互いに排反な4つの事象
\(A \cap \overline B\), \(A \cap B\), \(\overline A \cap B\), \(\overline A \cap \overline B\)
に分けられるので、確率の加法定理により
\(P(A)=P(A \cap \overline B)+P(A \cap B)\)・・・①
\(P(B)=P(\overline A \cap B)+P(A \cap B)\)・・・②
や、\(P(A \cup B)=\)\(P(A \cap \overline B)+P(A \cap B)+P(\overline A \cap B)\) から
\(P(A \cup B)=P(A)+P(\overline A \cap B)\)・・・③
\(P(A \cup B)=P(B)+P(A \cap \overline B)\)・・・④
などが成り立ちます。
①~④は覚えなくてよいです。
やってることは集合の要素の個数を数えることと同じなので (要素の個数の等式の両辺を全事象の場合の数\(n(U)\)で割ると確率になる)、ベン図を書いてパズルのように各領域を足したり引いたりして、求めたい確率を出します。
やってることは集合の要素の個数を数えることと同じなので (要素の個数の等式の両辺を全事象の場合の数\(n(U)\)で割ると確率になる)、ベン図を書いてパズルのように各領域を足したり引いたりして、求めたい確率を出します。
(例題)
\(n\)個 \((n≧2)\)のさいころを1度に投げるとき、1の目が少なくとも1つ出るという事象を\(A\)、偶数の目が少なくとも1つ出るという事象を\(B\)、\(A\)も\(B\)も起こらないという事象を\(C\)とする。このとき次の確率を求めよ。
(1)\(A,B,C\)のおのおのについて、それが起こる確率
(2)\(A\) または \(B\)が起こる確率
(3)\(A\)は起こるが\(B\)は起こらない確率
(4)\(A\)も\(B\)も起こる確率
\(n\)個 \((n≧2)\)のさいころを1度に投げるとき、1の目が少なくとも1つ出るという事象を\(A\)、偶数の目が少なくとも1つ出るという事象を\(B\)、\(A\)も\(B\)も起こらないという事象を\(C\)とする。このとき次の確率を求めよ。
(1)\(A,B,C\)のおのおのについて、それが起こる確率
(2)\(A\) または \(B\)が起こる確率
(3)\(A\)は起こるが\(B\)は起こらない確率
(4)\(A\)も\(B\)も起こる確率
(解答)
(1)
\(A,B\)は余事象を考えます。
\(C\)は、\(\overline A \cap \overline B\) なので、「1つも1の目が出ない かつ 1つも偶数の目が出ない」事象となります。
\(C\)は、\(\overline A \cap \overline B\) なので、「1つも1の目が出ない かつ 1つも偶数の目が出ない」事象となります。
\(\overline A\) は「1つも1が出ない」という事象なので
\(P(A)=1-P(\overline A)=1-\displaystyle\frac{5^n}{6^n}=\)\(1-(\displaystyle\frac{5}{6})^n\)
同様に、\(\overline B\) を考えて
\(P(B)=1-P(\overline B)=1-\displaystyle\frac{3^n}{6^n}=\)\(1-(\displaystyle\frac{1}{2})^n\)
\(P(B)=1-P(\overline B)=1-\displaystyle\frac{3^n}{6^n}=\)\(1-(\displaystyle\frac{1}{2})^n\)
\(C\)は、\(\overline A \cap \overline B\) なので、3,5の目だけが出る場合を考えて
\(P(C)=\displaystyle\frac{2^n}{6^n}=\)\((\displaystyle\frac{1}{3})^n\)
\(P(C)=\displaystyle\frac{2^n}{6^n}=\)\((\displaystyle\frac{1}{3})^n\)
(2)
直接\(P(A \cup B)\)を求めるのは大変そうなので、余事象を考えます。
ここでド・モルガンの法則を使うと、式に\(P(C)\)が表れます。
ここでド・モルガンの法則を使うと、式に\(P(C)\)が表れます。
\(P(A \cup B)=1-P(\overline{A \cup B})\)\(=1-P(\overline A \cap \overline B)=1-P(C)\)
\(=\)\(1-(\displaystyle\frac{1}{3})^n\)
\(=\)\(1-(\displaystyle\frac{1}{3})^n\)
(3)
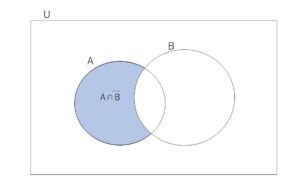
求めるものは、\(P(A \cap \overline B)\)です。
ベン図で考えてみます。(結局先ほど述べた④を使うことになる)
ベン図で考えてみます。(結局先ほど述べた④を使うことになる)
図より、
\(P(A \cap \overline B)=P(A \cup B)-P(B)\)
\(P(A \cap \overline B)=P(A \cup B)-P(B)\)
よって(1)(2)の結果から
\(P(A \cap \overline B)\)
\(=\{1-(\displaystyle\frac{1}{3})^n\}-\{1-(\displaystyle\frac{1}{2})^n\}\)
\(=\)\((\displaystyle\frac{1}{2})^n-(\displaystyle\frac{1}{3})^n\)
\(P(A \cap \overline B)\)
\(=\{1-(\displaystyle\frac{1}{3})^n\}-\{1-(\displaystyle\frac{1}{2})^n\}\)
\(=\)\((\displaystyle\frac{1}{2})^n-(\displaystyle\frac{1}{3})^n\)
(4)
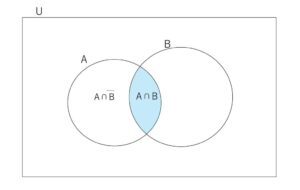
(3)と同様にベン図を考えてみます。
図より、
\(P(A \cap B)=P(A)-P(A \cap \overline B)\)
\(P(A \cap B)=P(A)-P(A \cap \overline B)\)
よって、(1)(3)から
\(P(A \cap B)\)
\(=\{1-(\displaystyle\frac{5}{6})^n\}-\{(\displaystyle\frac{1}{2})^n-(\displaystyle\frac{1}{3})^n\}\)
\(P(A \cap B)\)
\(=\{1-(\displaystyle\frac{5}{6})^n\}-\{(\displaystyle\frac{1}{2})^n-(\displaystyle\frac{1}{3})^n\}\)
\(=\)\(1+(\displaystyle\frac{1}{3})^n-(\displaystyle\frac{5}{6})^n-(\displaystyle\frac{1}{2})^n\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。