・独立な試行の確率
1個のさいころを投げる試行と、1枚の硬貨を投げる試行において、さいころの目の出方と、硬貨の裏表の出方は無関係であり、この2つの試行は互いにその結果に影響を及ぼしません。このように2つの試行が互いに他方の結果に影響を及ぼさないときこれらの試行は独立であるといいます。
排反も独立もお互い何も関係がなさそうというイメージは同じですが、
排反は「2つの事象が同時に起こらないこと」で、意味は違います。
\(p=\displaystyle\frac{4×1}{6×2}=\displaystyle\frac{4}{6}×\displaystyle\frac{1}{2}\) となります。
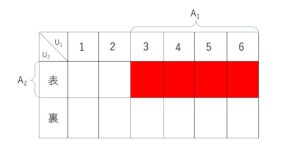
ここで、さいころを投げる試行を\(T_1\)、硬貨を投げる試行を\(T_2\)として、それぞれの試行での全事象を\(U_1,U_2\) します。また、\(T_1\)で3以上の目が出るという事象を\(A_1\)、\(T_2\)で表が出るという事象を\(A_2\)として、\(A_1\)と\(A_2\)が同時に起こる、つまり\(T_1,T_2\)を行い、さいころは3以上の目が出て、硬貨は表がでるという事象を\(A\)とします。
全事象\(U\)について、
\(n(U)=n(U_1)×n(U_2)\) (\(12=6×2\))
事象\(A\)について
\(n(A)=n(A_1)×n(A_2)\) (\(4=4×1\))
が成り立ち、\(U\)の根元事象は同様に確からしいので
\(p=P(A)\)を求めると
\(P(A)=\displaystyle\frac{n(A)}{n(U)}\)
\(=\displaystyle\frac{n(A_1)×n(A_2)}{n(U_1)×n(U_2)}\)
\(=\displaystyle\frac{n(A_1)}{n(U_1)}×\displaystyle\frac{n(A_2)}{n(U_2)}\)
\(=P(A_1)×P(A_2)\)
今述べたことは一般的に2つの独立な試行について成り立つ。
\(P(A)=P(A_1)×P(A_2)\)
例でいうと、「さいころは3以上の目が出て、硬貨は表が出る」確率は、
(さいころで3以上の目が出る確率)×(硬貨で表が出る確率)
ということです。
1つのサイコロを2回投げるとき、1回目と2回目ともに1の目が出る確率
サイコロは毎回等確率で6つのどれかの目が出ます。
2回のサイコロを投げる試行は互いに独立。よって
\(p=\displaystyle\frac{1}{6}×\displaystyle\frac{1}{6}=\)\(\displaystyle\frac{1}{36}\)
3つ以上の試行においても、どの試行の結果も他の試行の結果に影響を及ぼさないとき、これらの試行は独立であるといいます。例えば3回さいころを投げるときの各さいころを投げる試行は独立です。
3つの独立な試行\(T_1,T_2,T_3\)において、\(T_1\)で事象\(A_1\)が起こり、\(T_2\)で事象\(A_2\)が起こり、\(T_3\)で事象\(A_3\)が起こるという事象を\(A\)とすると、2つの独立な試行の場合と同様に
4つ以上の独立な試行についても同様の等式が成り立ちます。
(独立な試行)
①さいころを投げる試行と硬貨を投げる試行
②さいころを複数回投げるときの各さいころを投げる試行どうし
③赤球と白球が複数入った袋の中から、玉を1個取り出す試行を\(T_1\)、続いて球を取り出す試行を\(T_2\)としたとき、最初の球を袋に戻すときの \(T_1,T_2\)
(独立な試行ではない)
③において、最初の球を袋に戻さないときの\(T_1,T_2\)
など
3人の射手A,B,Cが標的に向かって射つとき、当てる確率はそれぞれ、\(\displaystyle\frac{1}{2}\),\(\displaystyle\frac{1}{3}\),\(\displaystyle\frac{1}{4}\) であるという。このとき少なくとも1人が当てる確率を求めよ。
つまり3人の当たる当たらないという結果は互いに影響を及ぼさないことになります。
少なくとも1人が当てる確率なので、1人も当たらない確率(余事象の確率)を求めて解いてみます。
A,B,Cが射つという試行において、それぞれが当たらないことは互いに独立であると考えられるから、3人とも当たらない確率は
\((1-\displaystyle\frac{1}{2})(1-\displaystyle\frac{1}{3})(1-\displaystyle\frac{1}{4})=\displaystyle\frac{1}{4}\)
\(1-\displaystyle\frac{1}{4}=\)\(\displaystyle\frac{3}{4}\)
A,Bの2つの袋があり、Aには赤球3個と白球5個、Bには赤球6個と白球4個が入っている。A,Bの袋から1つずつ球を取り出すとき、取り出した2個の球の色が同じである確率を求めよ。
袋Aから球を取り出す試行と、袋Bから球を取り出す試行は独立である。
①2個とも赤色 ②2個とも白色
のいずれかで、これらは排反である。
①について
それぞれの袋から赤球を取り出す確率を考えると
\(\displaystyle\frac{3}{8}×\displaystyle\frac{6}{10}=\displaystyle\frac{18}{80}\)
\(\displaystyle\frac{5}{8}×\displaystyle\frac{4}{10}=\displaystyle\frac{20}{80}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。