・反復試行の確率
さいころを何回も続けて投げるような、独立な試行の繰り返しを反復試行といいます。
次の具体的な例を考えてみて、反復試行の確率を求める公式を導いてみます。
1個のさいころを5回続けて投げる反復試行において、6の目がちょうど2回でる確率を求めよ。
例えば、6の目が1回目と4回目に出るとします。他の2,3,5回目は6以外の目が出ることになるのでその確率は、
\(\displaystyle\frac{1}{6}×\displaystyle\frac{5}{6}×\displaystyle\frac{5}{6}×\displaystyle\frac{1}{6}×\displaystyle\frac{5}{6}=(\displaystyle\frac{1}{6})^2(\displaystyle\frac{5}{6})^3\)・・・①
です。
今1回目と4回目に6の目が出る場合を考えましたが、他にも例えば2,3回目などといった6の目の出方のパターンがありますね。全部で何パターンあるかというと、5回投げるということを5つの「○」で考えて、そのうちの2つの「〇」の選び方だけあるので、\({}_5\mathrm{C}_2\) 通りです。
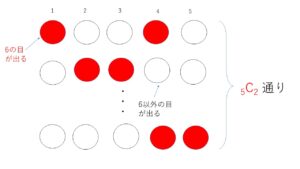
この\({}_5\mathrm{C}_2\) 通りおのおのが起こる確率は、①と同じ\((\displaystyle\frac{1}{6})^2(\displaystyle\frac{5}{6})^3\)であり、\({}_5\mathrm{C}_2\) 通りの事象は互いに排反なので、求める確率は
\({}_5\mathrm{C}_2(\displaystyle\frac{1}{6})^2(\displaystyle\frac{5}{6})^3\)
となります。
これと全く同じ考えで一般的な場合についての反復試行の確率を求めることができます。
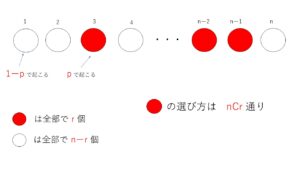
1回の試行で事象\(A\)が起こる確率を\(p\)として、この試行を\(n\)回行うとき、事象\(A\)がちょうど\(r\)回起こる確率を考えます。
まず、\(n\)個の「〇」の中から、\(r\)個選ぶ方法を考えると、
\({}_n\mathrm{C}_r\) 通り。
また、そのおのおのの起こる確率は、事象\(A\)が起こらない回数が\(n-r\)回で、その確率が\(1-p\)であることから
\(p^r(1-p)^{n-r}\)
また、これら\({}_n\mathrm{C}_r\) 通りの事象は互いに排反。
よって、事象\(A\)がちょうど\(r\)回起こる確率は
\({}_n\mathrm{C}_rp^r(1-p)^{n-r}\)
となります。
という公式は覚えるのではなく導けるようにしましょう。
赤球4個と白球2個がはいっている袋から1球を取り出して、球の色を見て袋に戻す。この試行を4回繰り返したとき、赤球がちょうど3回でる確率を求めよ。
1回の試行で
赤球が取り出される確率は\(\displaystyle\frac{4}{6}\)で、赤球が取り出されない確率は\(1-\displaystyle\frac{4}{6}\)\(=\displaystyle\frac{2}{6}\)
よって求める確率は
\({}_4\mathrm{C}_3(\displaystyle\frac{4}{6})^3(\displaystyle\frac{2}{6})=\)\(\displaystyle\frac{32}{81}\)
正しいものには〇印を、正しくないものには×印をつける、いわゆる〇×式の問題が10問ある。〇印と×印をでたらめにつけるとき、少なくとも3問が正解となる確率を求めよ。
直接3問以上正解となる(3~10問正解となる)確率を求めるのは大変なので、余事象を考えます。
正解の問題数が0,1,2の場合を考える。
\({}_{10}\mathrm{C}_r(\displaystyle\frac{1}{2})^r(\displaystyle\frac{1}{2})^{10-r}=\displaystyle\frac{{}_{10}\mathrm{C}_r}{2^{10}}\)
\(\displaystyle\frac{{}_{10}\mathrm{C}_0+{}_{10}\mathrm{C}_1+{}_{10}\mathrm{C}_2}{2^{10}}=\displaystyle\frac{7}{128}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。