円周上を動く点の確率に関する問題について見ていきます。
円なので、最初いた点に戻ってくることがあります。
(例題)
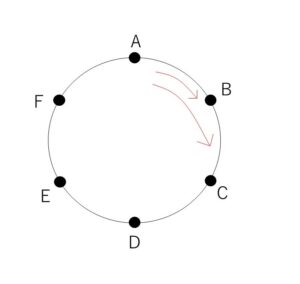
円周上を6等分する点を時計回りの順にA,B,C,D,E,Fとし、点Aを出発点として小石をおく。さいころを振り、偶数の目が出たときは2、奇数の目が出たときは1だけ小石を時計回りに分点上を進めるゲームを続け、最初に点Aに戻ったときを上がりとする。次の確率を求めよ。
(1)ちょうど1周して上がる確率
(2)ちょうど2週して上がる確率
(解答)
(1)
偶数,奇数の目が出る回数を、\(s,t\)として方程式を立てます。
6等分された弧の長さを1とすれば、6だけ進むことになるので
\(2s+t=6\) (\(s,t\)は\(0\)以上の整数)となります。\(s\)に具体的な数字を0から代入して\(s,t\)を求めましょう。
6等分された弧の長さを1とすれば、6だけ進むことになるので
\(2s+t=6\) (\(s,t\)は\(0\)以上の整数)となります。\(s\)に具体的な数字を0から代入して\(s,t\)を求めましょう。

ちょうど1週して上がるのは、偶数,奇数の目が出る回数を、\(s,t\)とすれば
\(2s+t=6\) (\(s,t\)は\(0\)以上の整数)
これを解くと
\((s,t)=(0,6),(1,4),(2,2),(3,0)\)
\(2s+t=6\) (\(s,t\)は\(0\)以上の整数)
これを解くと
\((s,t)=(0,6),(1,4),(2,2),(3,0)\)
よって、求める確率は、それぞれの場合を考えて
\({}_6\mathrm{C}_0(\displaystyle\frac{1}{2})^6+{}_5\mathrm{C}_1(\displaystyle\frac{1}{2})^5+\)\({}_4\mathrm{C}_2(\displaystyle\frac{1}{2})^4+{}_3\mathrm{C}_0(\displaystyle\frac{1}{2})^3\)
\(=\)\(\displaystyle\frac{43}{64}\)
\(=\)\(\displaystyle\frac{43}{64}\)
(2)
ちょうど2周してあがるには、1週目でAを通過することになります。よって
①A→F ②F→B ③B→A
の経路を考えることになります。
①A→F ②F→B ③B→A
の経路を考えることになります。
ちょうど2周してあがるには、
①Aから出発して、Fにつく
②Fから出発して、Aを通過してBにつく
③Bから出発して、Aにつく
経路を考えればよい。
①Aから出発して、Fにつく
②Fから出発して、Aを通過してBにつく
③Bから出発して、Aにつく
経路を考えればよい。
①について
偶数,奇数の目が出る回数を、\(s,t\)とすれば
\(2s+t=5\) (\(s,t\)は\(0\)以上の整数)
これを解くと
\((s,t)=(0,5),(1,3),(2,1)\)
よって ①の確率は
\({}_5\mathrm{C}_0(\displaystyle\frac{1}{2})^5+{}_4\mathrm{C}_1(\displaystyle\frac{1}{2})^4+\)\({}_3\mathrm{C}_2(\displaystyle\frac{1}{2})^3\)
\(=\)\(\displaystyle\frac{21}{32}\)
偶数,奇数の目が出る回数を、\(s,t\)とすれば
\(2s+t=5\) (\(s,t\)は\(0\)以上の整数)
これを解くと
\((s,t)=(0,5),(1,3),(2,1)\)
よって ①の確率は
\({}_5\mathrm{C}_0(\displaystyle\frac{1}{2})^5+{}_4\mathrm{C}_1(\displaystyle\frac{1}{2})^4+\)\({}_3\mathrm{C}_2(\displaystyle\frac{1}{2})^3\)
\(=\)\(\displaystyle\frac{21}{32}\)
②について
偶数の目が出ればよいので、確率は \(\displaystyle\frac{1}{2}\)
偶数の目が出ればよいので、確率は \(\displaystyle\frac{1}{2}\)
③について
偶数,奇数の目が出る回数を、\(s,t\)とすれば
\(2s+t=5\) (\(s,t\)は\(0\)以上の整数)
であり、①と同じなので、その確率は \(\displaystyle\frac{21}{32}\)
偶数,奇数の目が出る回数を、\(s,t\)とすれば
\(2s+t=5\) (\(s,t\)は\(0\)以上の整数)
であり、①と同じなので、その確率は \(\displaystyle\frac{21}{32}\)
以上①~③より、求める確率は
\(\displaystyle\frac{21}{32}×\displaystyle\frac{1}{2}×\displaystyle\frac{21}{32}\)
\(\displaystyle\frac{21}{32}×\displaystyle\frac{1}{2}×\displaystyle\frac{21}{32}\)
\(=\)\(\displaystyle\frac{441}{2048}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。