赤玉5個とと白玉が10個入っている袋から、1個ずつ玉を取り出す(ただし毎回玉を袋に戻す)操作で、14回のうち5回赤玉が出る確率は、反復試行の確率を利用して求めることができます。では、玉を毎回戻さない場合の確率はどうやって求めることができるのでしょうか。
まずは次の問題について考えてみます。
(例題1)
袋の中に白球4個と黒球5個とが入っている。この袋から1球ずつ取り出し、もとへ戻さないとする。すべてを取り出すとき、異なる色の球が交互に出る確率を求めよ。
まずは、確率の乗法定理を使って求めてみます。
つまり、1回1回の球の取り出される確率を考えます。(9回分なので式が長くなります)
つまり、1回1回の球の取り出される確率を考えます。(9回分なので式が長くなります)
(解答)
異なる色の球が交互に出る場合は、黒白黒白黒白黒白黒 と出る場合のみなので、乗法定理より
\(\displaystyle\frac{5}{9}・\displaystyle\frac{4}{8}・\displaystyle\frac{4}{7}・\displaystyle\frac{3}{6}・\displaystyle\frac{3}{5}\)\(・\displaystyle\frac{2}{4}・\displaystyle\frac{2}{3}・\displaystyle\frac{1}{2}・\displaystyle\frac{1}{1}\)\(=\)\(\displaystyle\frac{1}{126}\)
異なる色の球が交互に出る場合は、黒白黒白黒白黒白黒 と出る場合のみなので、乗法定理より
\(\displaystyle\frac{5}{9}・\displaystyle\frac{4}{8}・\displaystyle\frac{4}{7}・\displaystyle\frac{3}{6}・\displaystyle\frac{3}{5}\)\(・\displaystyle\frac{2}{4}・\displaystyle\frac{2}{3}・\displaystyle\frac{1}{2}・\displaystyle\frac{1}{1}\)\(=\)\(\displaystyle\frac{1}{126}\)
答えは出ます。
ただ、この方法だと式が長くなるし、取り出す回数が多くなると大変になってしまいます。
ただ、この方法だと式が長くなるし、取り出す回数が多くなると大変になってしまいます。
続いて次の問題について考えてみます。
(例題2)
赤玉5個と白玉10個が入っている袋の中から無作為に1個ずつ取り出す操作を続ける。ただし、取り出した玉は袋には戻さないものとする。このとき赤玉が先に袋の中になくなる確率を求めよ。
乗法定理を用いるならば、赤玉がなくなる回数を考えると、
5回,6回,7回・・・14回
となり全部の場合を考えることになり大変です。
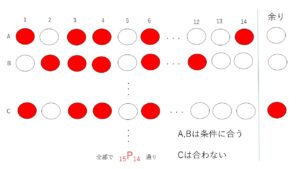
そこで、「赤玉が先に袋の中になくなる=14回引くまでに赤玉5個全部取り出す」と考えます。「14回引くまでに赤玉5個全部取り出す確率」は、「14回引くとき赤玉が5回出る確率・・・①」と同じなので、①を求めます。
①くらいなら乗法定理でごり押せそうですが、別の方法を検討します。
①を求める際に、15個の中から(球を戻さずに)14回玉を引くということを、15個の中から14個選んで並べる(順列)として、並べた順番と引いた順番を対応させます。全事象の場合の数 \({}_{15}\mathrm{P}_{14}\) は、同様に確からしいので、このうち、14番目までに赤玉が5個ある場合を考えれば、求める確率が分かります。
5回,6回,7回・・・14回
となり全部の場合を考えることになり大変です。
そこで、「赤玉が先に袋の中になくなる=14回引くまでに赤玉5個全部取り出す」と考えます。「14回引くまでに赤玉5個全部取り出す確率」は、「14回引くとき赤玉が5回出る確率・・・①」と同じなので、①を求めます。
①くらいなら乗法定理でごり押せそうですが、別の方法を検討します。
①を求める際に、15個の中から(球を戻さずに)14回玉を引くということを、15個の中から14個選んで並べる(順列)として、並べた順番と引いた順番を対応させます。全事象の場合の数 \({}_{15}\mathrm{P}_{14}\) は、同様に確からしいので、このうち、14番目までに赤玉が5個ある場合を考えれば、求める確率が分かります。

念のため確認ですが、赤5個と白10個は、15個すべて区別できるものとして考えるのが原則です。
(解答)
求める確率は、14回引くときに赤玉が5回出る確率である。15個の中から14回引くことを、異なる15個の玉から14個取り出して並べる順列として、その並べる順番と引く順番を対応させる。
全部の並べ方は、\({}_{15}\mathrm{P}_{14}\) 通りで、そのうち14番目までに5個の赤玉がある場合は、
\({}_5\mathrm{C}_5×{}_{10}\mathrm{C}_9×14!\) 通り
求める確率は、14回引くときに赤玉が5回出る確率である。15個の中から14回引くことを、異なる15個の玉から14個取り出して並べる順列として、その並べる順番と引く順番を対応させる。
全部の並べ方は、\({}_{15}\mathrm{P}_{14}\) 通りで、そのうち14番目までに5個の赤玉がある場合は、
\({}_5\mathrm{C}_5×{}_{10}\mathrm{C}_9×14!\) 通り
よって、求める確率は
\(\displaystyle\frac{{}_5\mathrm{C}_5×{}_{10}\mathrm{C}_9×14!}{{}_{15}\mathrm{P}_{14}}=\)\(\displaystyle\frac{2}{3}\)
\(\displaystyle\frac{{}_5\mathrm{C}_5×{}_{10}\mathrm{C}_9×14!}{{}_{15}\mathrm{P}_{14}}=\)\(\displaystyle\frac{2}{3}\)
最後に例題1も順列を使って求めてみます。
(例題1 別解)
白球4個と黒球5個の合計9個を並べる順列を考えて、並べる順番と取り出す順番を対応させる。全部の並べ方は \(9!\) 通りで、条件に合う並べ方は、黒白黒白黒白黒白黒 の場合だけなので、\(5!×4!\) 通り。よって求める確率は
\(\displaystyle\frac{5!4!}{9!}=\)\(\displaystyle\frac{1}{126}\)
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。