命題の真偽を判定する際に集合を考えると分かりやすい場合があります。
・条件と集合
(命題) \(x>3\) ならば \(x>1\) \(p→q\)
この命題は真です。ここで2つの集合
\(P=\{x|x>3\}\)、\(Q=\{x|x>1\}\)
を考えると、\(P\subset Q\) となります。
同様に考えると、一般的に2つの条件 \(p,q\) について、\(p\)を満たすもの全体の集合を\(P\)、\(q\)を満たすもの全体の集合を\(Q\)とすれば、
\(p→q\)が真ならば、\(P\subset Q\)であるといえます。
逆に\(P\subset Q\)ならば、\(p\)を満たすものは必ず\(q\)を満たすので\(p→q\)が真であることになります。
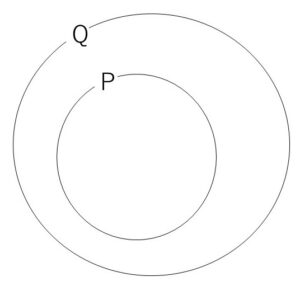
\(p→q\)が真 \(\leftrightarrow\) \(P\subset Q\)
※条件\(p\)のあらゆる要素について条件\(q\)が真となるので、\(Q\)のほうが広いイメージです。
\(q→p\)が真の場合も同じ事がいえます。
\(q→p\)が真 \(\leftrightarrow\) \(Q\subset P\)
\(p\leftrightarrow q\)が真のときは、\(P\subset Q\) かつ \(Q\subset P\) つまり\(P=Q\)のときで、
\(p\leftrightarrow q\)が真 \(\leftrightarrow\) \(P=Q\)
例題を解いてみましょう。
(例)次の命題の真偽を調べよ。
\(x<1\) ならば \(|x|<1\)
(解答)
\(P=\{x|x<1\}\), \(Q=\{x\) \(|\) \(|x|<1)\}\)とすると
\(Q=\{x|-1<x<1)\}\)となり
\(P\subset Q\)は成り立たない。
よって偽。
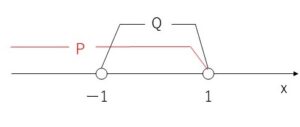
PのQからはみ出している部分、(\(x≦-1\))が反例です。
以上になります。お疲れさまでした。
ここまで読んで下さりありがとうございました。